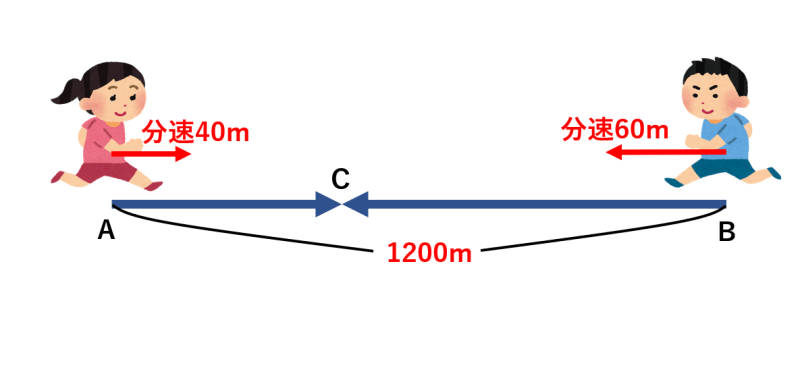
<円周上の旅人算1> ある池のまわりを1周するのに,兄は分,弟は30分かかります。 (1) この池のまわりを,2人が同じ地点から同時に反対方向に進みます。2人がはじめて出会うのは,出発してから何分後ですか。 (2)連立文章題速さ 出会う、追いつく 出会うときは、2人の距離の和、追いつくときは距離の差を考える A君とB君の2人は1400m離れた位置にいる。 2人が同時に出発して向かい合って歩くと10分後に出会う。 同じ方向に歩くとA君がB君に35分後に追いつく。 A君と旅人算は基本的に 2 2 人が 1 1 本の道を移動する状況に関して問題が出されます。 主に以下の 2 2 つが代表的です。 一方がもう一方を追いかける(追いつき算) 一本道の両端からそれぞれお互いを目指して出発する(出会い算) それぞれ具体的な例を

速さと比 旅人算の演習 受験算数アーカイブス
出会い算 池
出会い算 池- 旅人算(出会い) 旅人算(追いかけ)130 2のプリントの解答にミスがありましたので修正しました。旅人算(池のまわり) 旅人算(やや複雑な問題)分後に2人は出会いました。 (6) A君は毎分95m歩き、B君は毎分85m歩きます。今、2人が周囲の長さが2160mの池の周りを同時に同じ場所から反対方向に出発しました。 分後に2人は出会いました。



1
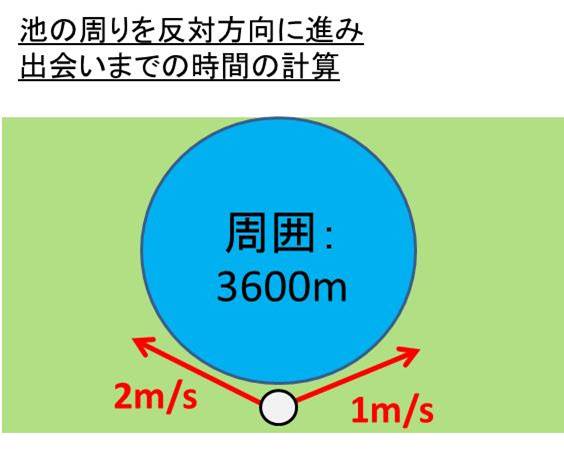
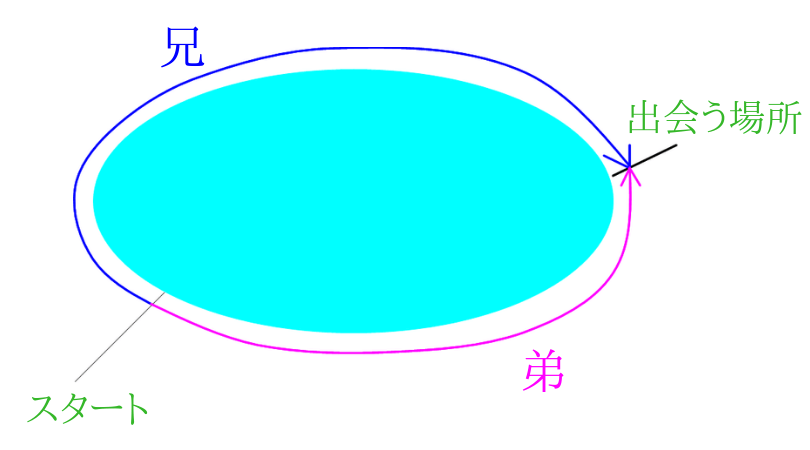
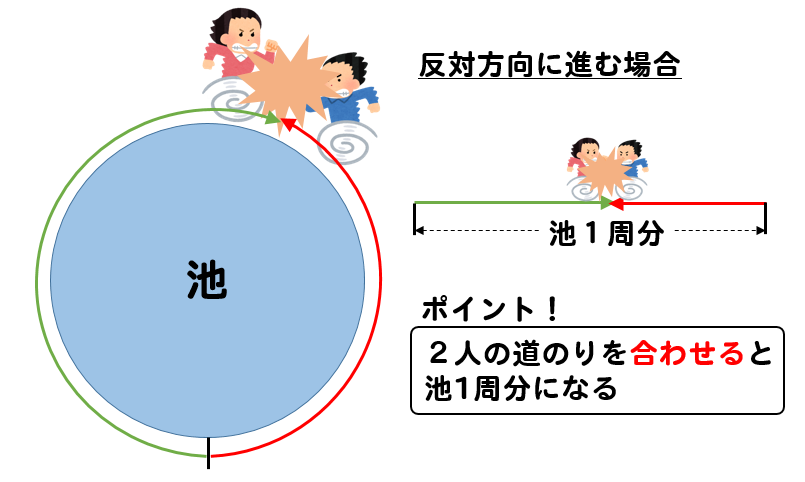
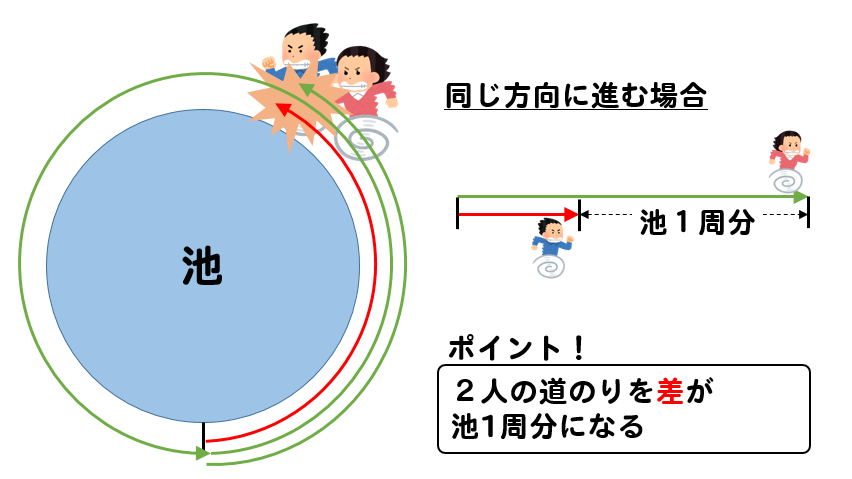
池の周りで出会う⇒2人の進んだ距離の和=池の周りの長さ 解答 2人が出発してから再び出会うまでの時間をx(分)とおく。 兄が進んだ距離は 弟が進んだ距離は 2人の進んだ距離の和が池の周りの長さと等しいので 60x+30x=3600 これを解いてO O O o EE 94 co — Fit o ms — EE El o o kJl EE ÙtH Created Date 7/1/ PM 旅人算の基本は、2人の距離の差や和、速さの差や和を考えます。 2人の距離の差は、池の1周分30mになりますので、30mの差を、何分でなくすことができるかを考えます。 そうすると分後に2人は道の途中で出会いました。
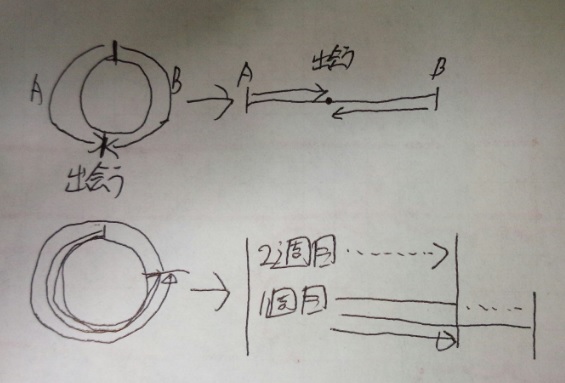
前回の問題をもう一度。 ≪問題≫ ある池の周りを兄と弟が反対方向にまわると10分ごとに出会い、 同じ方向にまわると兄が弟を50分ごとに追い越す。 兄と弟の速さの比(兄:弟)はいくらか? 兄と弟が出会うまでに移動した2人の距離の合計を考えていきます。 2人が出発して出会うまでに移動したそれぞれの距離の和は、池1周分の\ (10m\)です。 また2人の移動した距離の合計は1分ごとに\ (150m\)ずつ増えていきます。出会い算・追いつき算など種類別の 旅人算には「池の周りを回る」「グラウンドを走る」というように、 円形の動きをする問題もあります。 円形の動きをするという内容の旅人算は一周分の距離が明示されていないことが多く、一周するのにどのくらいの
はじめに 今回は旅人算(出会い算・追いつき算)に関して詳しく解説します。 速度に関する基本的な計算に関しては深く理解出来ている前提となります。まずはその部分を詳しくお知りになりたい方は、本ブログの別記事(コチラ)をご参照下さい。 では、解説を始めます。旅人算の池の周りを反対方向にまわる出会い算の解き方とコツ 練習問題 あるジョギングコースの同じ地点から兄と弟が同時に反対方向に走り出しました。 コースの長さは1周\(3km\)です。 兄が分速\(1m\)で走ると10分後に弟とすれ違い旅人算の先に出た人を追いかけて追いつくような追いつき算の練習問題 旅人算の池の周りを反対方向にまわる出会い算の解き方とコツ 旅人算の池の周りを同じ方向にまわる追い越し算の練習問題 旅人算の2地点から出発して出会う



1




旅人算 の問題の解き方 小学生に教えるための分かりやすい解説 数学fun
Post navigation 旅人算 真ん中 で出会う 7 Posted on by by 池のまわりで出会い追いつく問題の考え方(中学数学) 55 shun_ei 18年6月19日 1116 2人が池のまわりをまわって出会ったり追いついたりするとき、時間や速さや場所をたずねる問題があります。旅人算⑷ 2回目の出会い・追いこし 6 6 1周270mの池のまわりを、姉は毎分55m、妹は毎分25mで、同時に 同地点を同じ方向に出発し、何周もまわります。 ⑴ 姉が妹をはじめて追いこすのは( )分後




連立方程式 池の周りを同じ方向 反対方向に回る問題を解説 Youtube




中学受験 算数 動画解説 速さ 出会い算 追いつき算9 Youtube
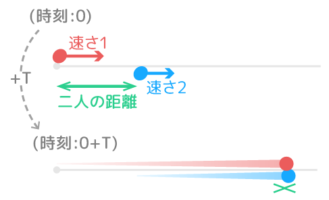
池一周分の、2人の出会いの旅人算が2通り与えられています。 池一周÷(兄の分速+弟の分速)=4分 池一周÷(兄の分速-40+弟の分速-8)=6分 上の2つの式のカッコの中の部分の比がわかります。 かかった時間の逆比です。旅人算③ 池の周りを逆向きに回って途中で出会う旅人算の解き方 「なぜ2人で池に来て、逆向きに回るのか!?普通は一緒に回るのではないか!?」 まったく意味の分からない設定ですが、なぜか算数の問題ではよく出題されます。一通り「なんでやねん。 こんにちは、ウチダです。 今日は中学受験算数講座第4回として 「旅人算」 について詳しく見ていきたいと思います。 旅人算の基本は「出会い算」「追いつき算」の $2$ つについてある共通点を見出すことです。 その共通点を見つけることで、今回用意した応用問題 $3$ つもかなり解き




旅人算の基本 図をかいて整理しよう




中学受験5年の壁 点の移動 攻略法を完全公開 たぶお Sapix サピックス A1 養成講座
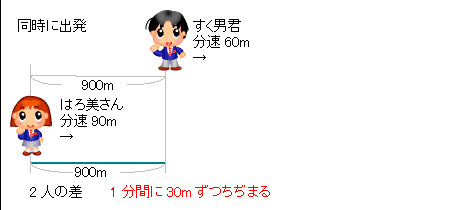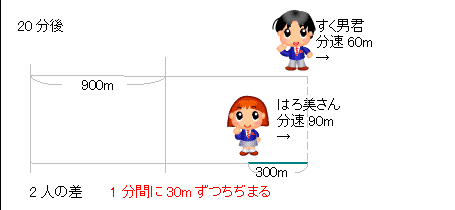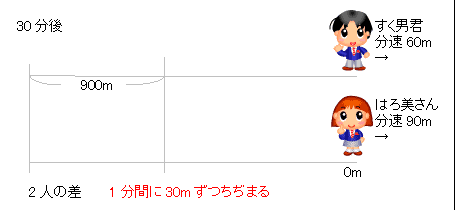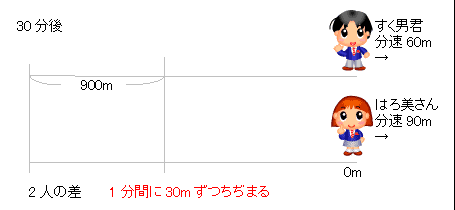
1-1 2人の進んだ距離の和=池1周の長さ 1-2 2人の速さの和×出会うのにかかる時間=池一周の長さ速さと比 (旅人算の演習) このページでは,旅人算としては比較的よく出題される『 池の周囲を回る問題 』の解法を確認したいと思います. まずは基本問題です. 問題1:池のまわりを1周するのに,太郎は分,次郎は30分かかります.太郎と次郎が反対ある池の周りをはろ美さんは分速75mで、すく男君は分速50mで、ある地点から同じ方向 に進みます。また、Yousuke先生は自転車に乗って分速250mの速さである地点から2人 と反対方向に進みます。3人が同時に出発して12分後にはろ美さんはYousukeに出会い ました。



3人旅人算 Wikipedia



旅人算 算数の教え上手 学びの場 Com
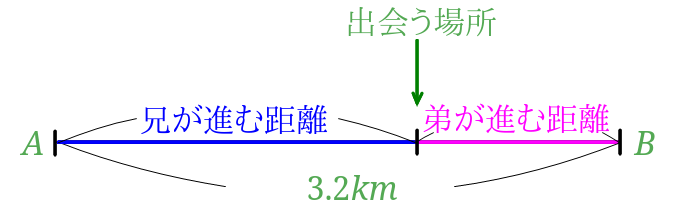
仕事算(何日で終わるか) 仕事算(合同作業) 植木算 年齢算(年数を求める) 年齢算(年齢を求める) 濃度算(混ぜる) 濃度算(薄める) 濃度算(濃くする) 流水算 旅人算(出会う時間) 旅人算(追いつく時間) 和差算 時計算(長針と短針の〈例題3〉3人の出会い算 池の周囲をA君とC君は同じ方向に, B君は反対方向に進みます。3人 の速さはA君が毎分 180m, B君は毎分 1m, C君は毎分100mです。 A君とB君が出会ってから 6分たってから, B君とC君が出会いました。 池1周は何mですか。小学校の算数でも 出会い算 として出題される問題です。 中学では方程式を使うことでこの問題を解きます。 出会ったときに2人が進んだ距離の合計は 問題文からポイントとなる箇所を抜き出します。 1周4.2km(4,0m) 兄分速160m




旅人算 問題の解説まとめ それぞれのパターンの解き方は 数スタ




例題あり 旅人算とは 出会い算 追いつき算など種類別の解き方や教え方のコツも解説 学びtimes



旅人算



基本 旅人算の解き方 テクニック 中学受験 塾なし の勉強法



中学受験 旅人算とは 基本公式から往復など応用問題 ダイヤグラムまで そうちゃ式 受験算数 2号館 図形 速さ



旅人算の問題16題をただひたすら解くページ 解き方もあり〼 チャンプルー
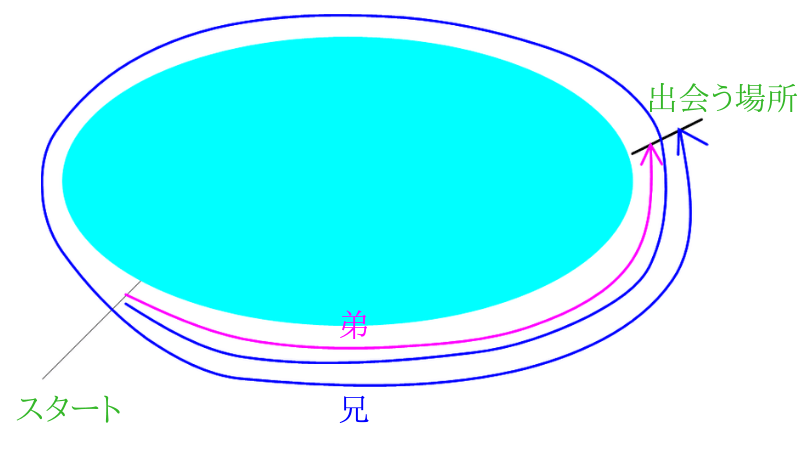



旅人算の苦手を克服 分かりやすく教える方法と解き方はコレ みけねこ小学校




旅人算の苦手を克服 分かりやすく教える方法と解き方はコレ みけねこ小学校




旅人算 の文章問題 計算ドリル 問題集 数学fun



旅人算の練習問題と解説 みけねこ小学校
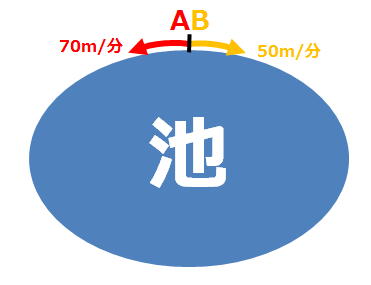



旅人算 池の周りを回る二人が出会う問題 の解き方




え こんなに簡単だったの 中学入試の分かりやすい旅人算の解き方 受験ボックス




え こんなに簡単だったの 中学入試の分かりやすい旅人算の解き方 受験ボックス




速さと比 ダイヤグラムで旅人算を図形的に考える 応用編 みみずく戦略室
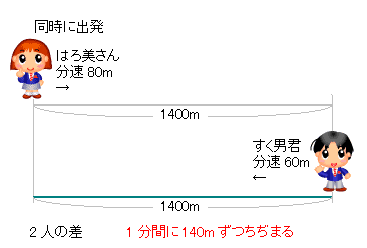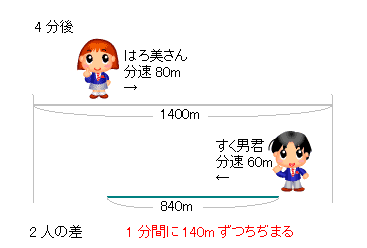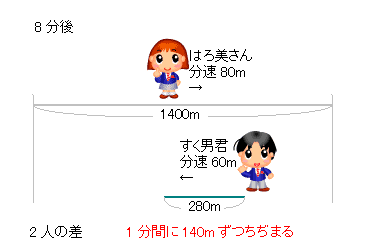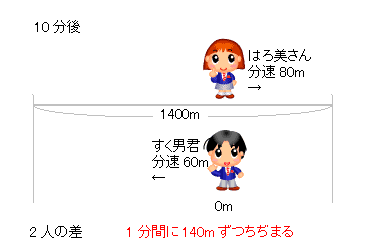



旅人算




旅人算 Youtube
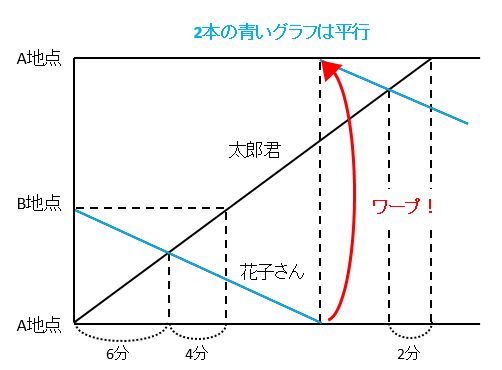



速さと比 ダイヤグラムで旅人算を図形的に考える 応用編 みみずく戦略室




池の周りをまわる旅人算の解き方と解説
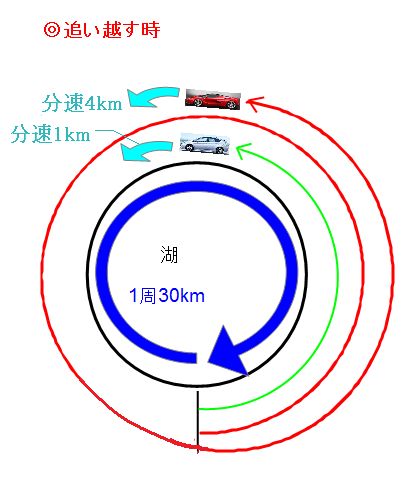



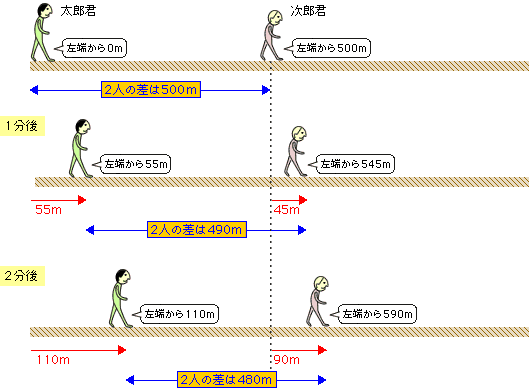
旅人算の4つの出題パターンを解説 1分後を意識すればすべて解ける




旅人算の基本 図をかいて整理しよう



例題あり 旅人算とは 出会い算 追いつき算など種類別の解き方や教え方のコツも解説 学びtimes



池の周りで出会う 追いつくなどの連立方程式の計算を行う方法 同じ方向 反対方向と速さ ウルトラフリーダム




旅人算ってどんなもの 旅人算をわかりやすく解説 中学受験ナビ



旅人算で間違いやすいポイントはココ



旅人算 問題の解説まとめ それぞれのパターンの解き方は 数スタ
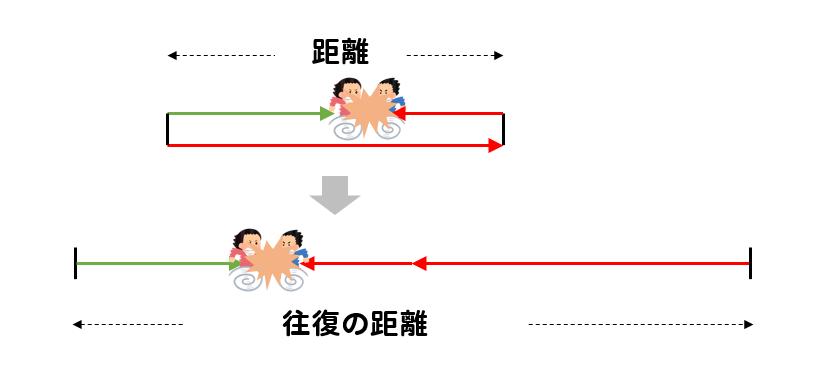



旅人算 往復するときの解き方は 2回目に出会うときは 数スタ




旅人算 池の周りで出会う問題の解き方 考え方 算数パラダイス




旅人算の解き方まとめ 公式から応用問題3選までわかりやすい解説 中学受験算数 遊ぶ数学




速さと比 旅人算の演習 受験算数アーカイブス




旅人算の基本公式をマスター




Spi中級上級編 18章 速度 旅人算 出会い算 追いつき算コラボ Youtube




え こんなに簡単だったの 中学入試の分かりやすい旅人算の解き方 受験ボックス




旅人算の基本 図をかいて整理しよう
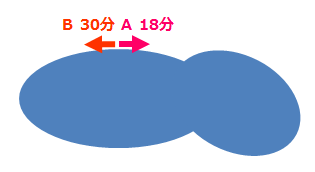



道のり 距離 が問題文にない旅人算の解き方




予習シリーズ算数5年上第19回 旅人算とグラフ 2 Youtube



1




中学数学 方程式 旅人算 追いつく Youtube



1
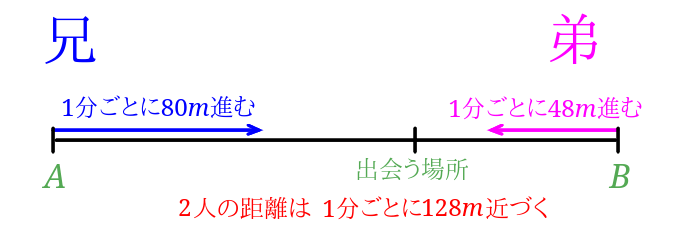



旅人算の苦手を克服 分かりやすく教える方法と解き方はコレ みけねこ小学校



1次方程式 速さ 中学から数学だいすき




円周上の旅人算を比で解く 2 速さと比 3 予習シリーズ5年下第11回 必修例題2 Youtube



旅人算 池の周りで追いつく問題の解き方 考え方 算数パラダイス




旅人算の4つの出題パターンを解説 1分後を意識すればすべて解ける




旅人算の基本 図をかいて整理しよう




旅人算に関する問題の解き方一覧 中学受験の算数 理科ヘクトパスカル



旅人算 中学受験ー算数解き方ポータル




旅人算 池の周りで出会う問題の解き方 考え方 算数パラダイス




旅人算 の問題の解き方 小学生に教えるための分かりやすい解説 数学fun




え こんなに簡単だったの 中学入試の分かりやすい旅人算の解き方 受験ボックス




旅人算の解き方まとめ 公式から応用問題3選までわかりやすい解説 中学受験算数 遊ぶ数学




例題あり 旅人算とは 出会い算 追いつき算など種類別の解き方や教え方のコツも解説 学びtimes



旅人算の苦手を克服 分かりやすく教える方法と解き方はコレ みけねこ小学校




速さ 旅人算 今日の一問 数的推理4 公試混同blog




旅人算の解き方まとめ 公式から応用問題3選までわかりやすい解説 中学受験算数 遊ぶ数学



旅人算の苦手を克服 分かりやすく教える方法と解き方はコレ みけねこ小学校




旅人算の解き方 中学受験の算数教室



速さ 算数解法の極意



算数 速さと比 1 中学受験 ベネッセ教育情報サイト
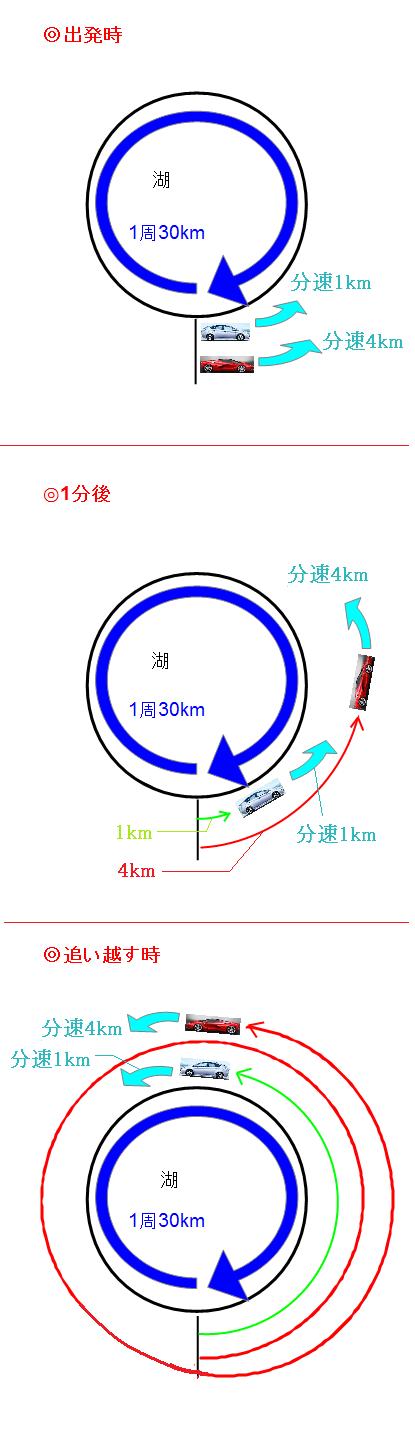



旅人算の4つの出題パターンを解説 1分後を意識すればすべて解ける



Math 中学受験 旅人算 発展問題 働きアリ




6月21日 小5算数 ジャングルジムブログ
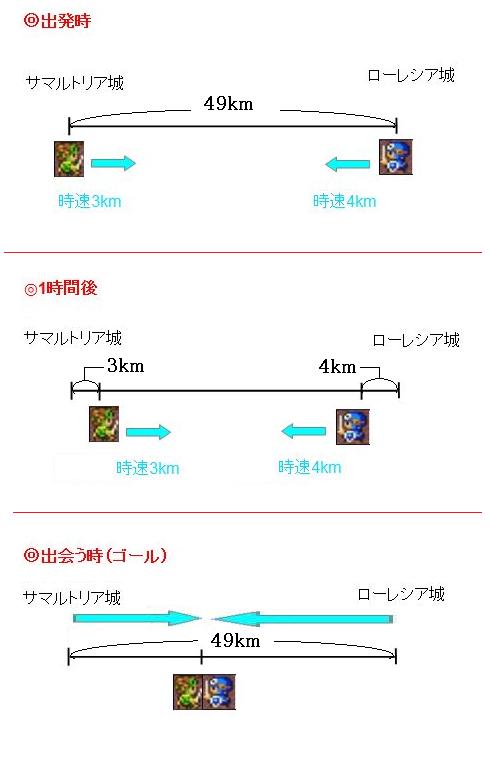



旅人算の4つの出題パターンを解説 1分後を意識すればすべて解ける




旅人算 往復するときの解き方は 2回目に出会うときは 数スタ
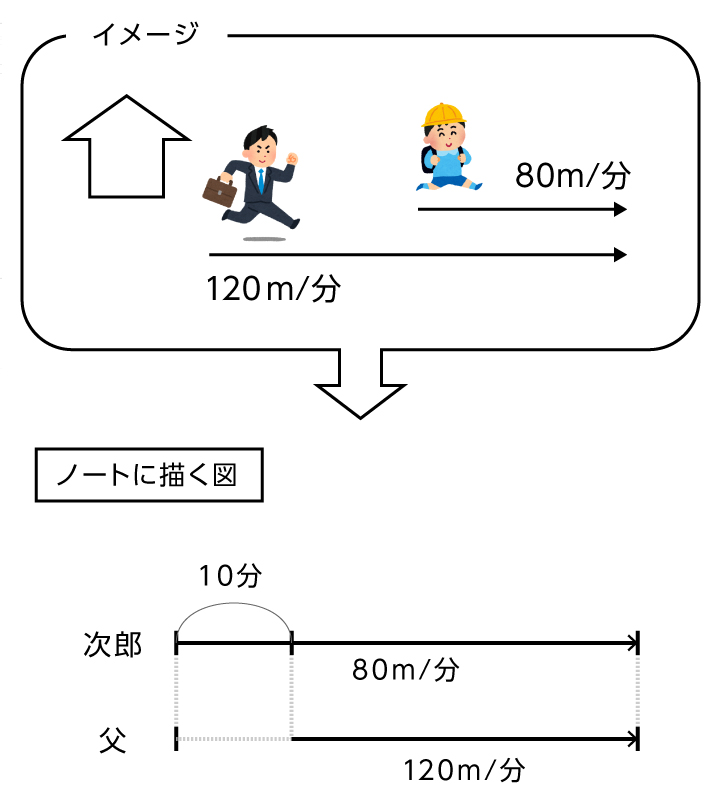



旅人算ってどんなもの 旅人算をわかりやすく解説 中学受験ナビ
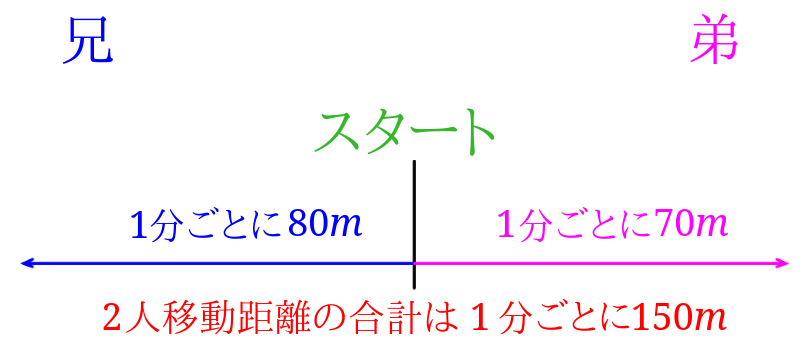



旅人算の苦手を克服 分かりやすく教える方法と解き方はコレ みけねこ小学校




旅人算 の問題の解き方 小学生に教えるための分かりやすい解説 数学fun
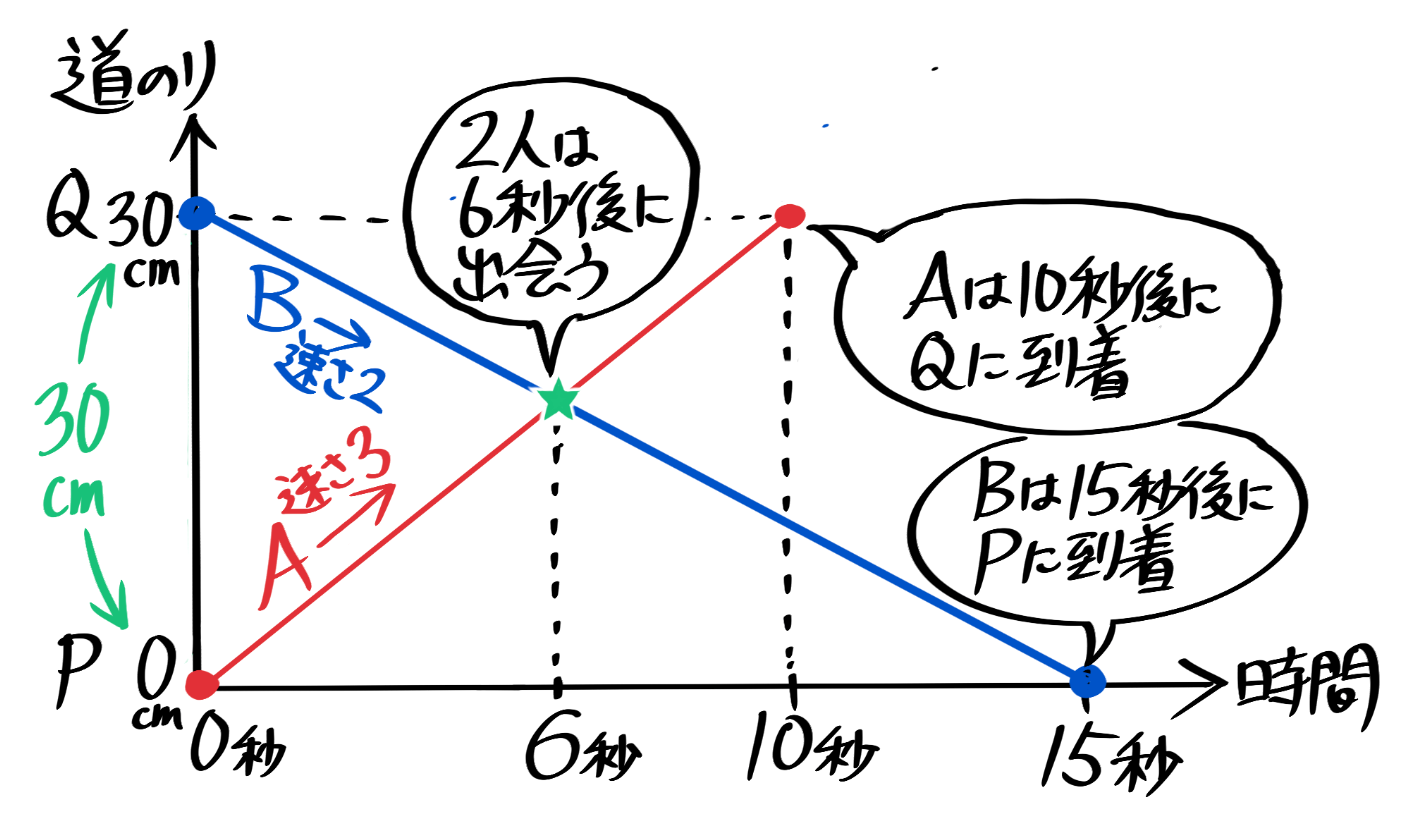



中学受験 旅人算とは 基本公式から往復など応用問題 ダイヤグラムまで そうちゃ式 受験算数 2号館 図形 速さ



1



旅人算 に挑戦してみよう part2




池の周りの旅人算 に挑戦 四天王寺中学校の入試問題から 親子で挑戦 中学受験算数 朝日新聞edua
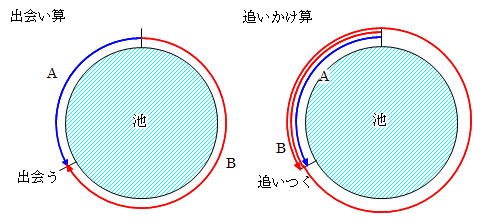



速さ 14 03 前田昌宏の中学受験が楽しくなる算数塾




旅人算の解き方まとめ 公式から応用問題3選までわかりやすい解説 中学受験算数 遊ぶ数学
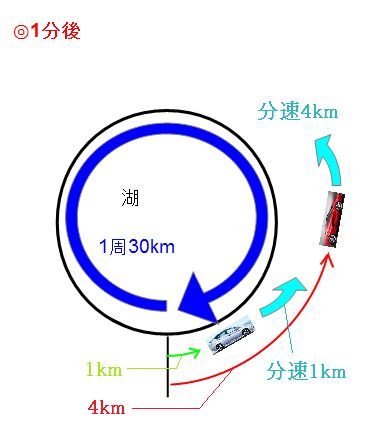



旅人算の4つの出題パターンを解説 1分後を意識すればすべて解ける




旅人算の基本 図をかいて整理しよう




旅人算の解き方まとめ 公式から応用問題3選までわかりやすい解説 中学受験算数 遊ぶ数学




Newみんなの算数講座7 自分で決めてよい池の長さ 中学受験の算数知恵宝庫
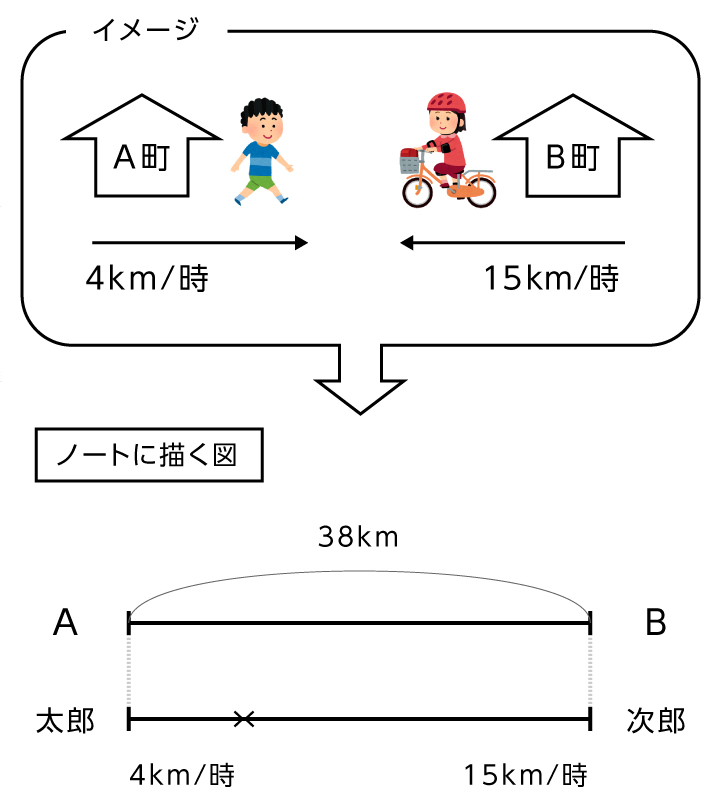



旅人算ってどんなもの 旅人算をわかりやすく解説 中学受験ナビ




印刷可能 中学受験 算数 速さ 旅人算



旅人算 問題の解説まとめ それぞれのパターンの解き方は 数スタ
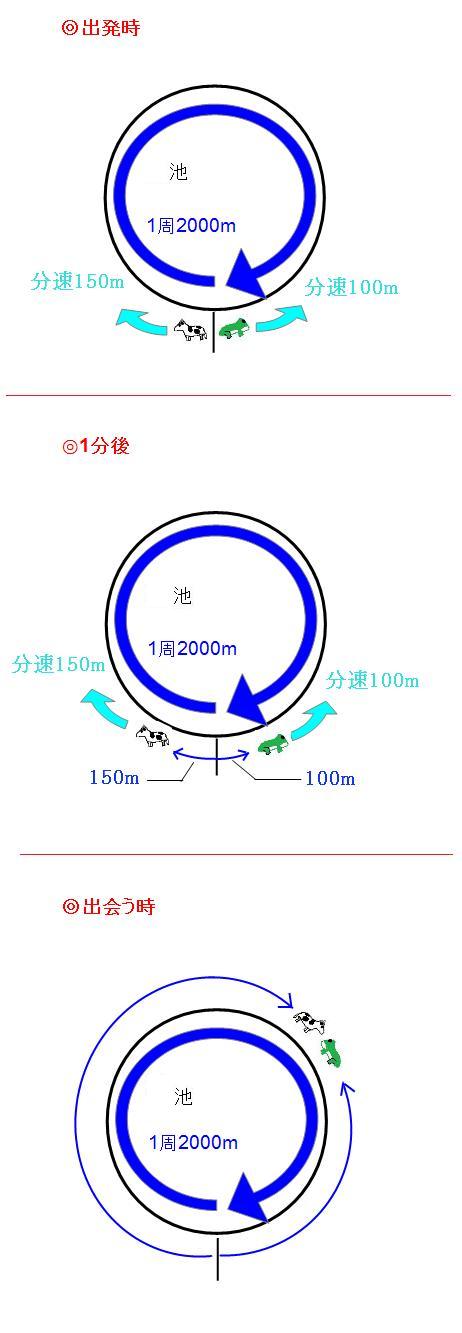



旅人算の4つの出題パターンを解説 1分後を意識すればすべて解ける




え こんなに簡単だったの 中学入試の分かりやすい旅人算の解き方 受験ボックス




印刷可能 中学受験 算数 速さ 旅人算




旅人算の4つの出題パターンを解説 1分後を意識すればすべて解ける
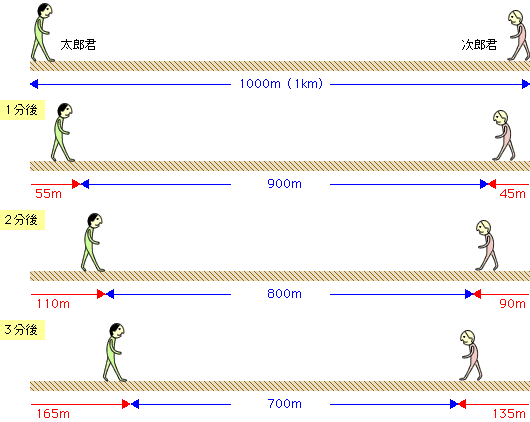



旅人算 算数の教え上手 学びの場 Com




旅人算 池の周りで追いつく問題の解き方 考え方 算数パラダイス



連立方程式 池の周りを追いつく速さの文章問題を解説 数スタ




バシッと解説中学受験算数 池の周りの旅人算 Youtube




旅人算の解き方まとめ 公式から応用問題3選までわかりやすい解説 中学受験算数 遊ぶ数学



旅人算がわかりません 問1周800mの池の周りをbさんとa君が同時に同じ Yahoo 知恵袋



旅人算 問題の解説まとめ それぞれのパターンの解き方は 数スタ




速さと比 旅人算の演習 受験算数アーカイブス



旅人算 出会い算 を算数の解法でお願いします 池のまわりを兄は14分で一周 Yahoo 知恵袋




旅人算の基本 図をかいて整理しよう



旅人算 中学受験ー算数解き方ポータル




速さ 旅人算 池の周りを歩く兄弟 中学受験算数 オンライン授業 数学 Youtube



基本 旅人算の解き方 テクニック 中学受験 塾なし の勉強法



0 件のコメント:
コメントを投稿