ひし形の面積は?求め方 ひし形の面積の求め方は 縦の対角線×横の対角線÷2 です。下図をみてください。これがひし形です。ひし形とは全ての辺の長さが等しい四角形です。またひし形の2つの対角線は必ず直交します。A^2b^2=c^2 a2 b2 = c2 英語ですが,三平方の定理の証明を105個解説しているすさまじいサイトがあります。 →Pythagorean Theorem 105個の中で,個人的に「簡単で美しい」と思った証明を4つ(#3,6,42,47)ほど紹介します。 目次 正方形を用いた証明 相似を用いた長方形・ひし形は平行四辺形の一種なので、平行四辺形の対角線の性質を持っています。 さらに、『すべての角が直角』の長方形と『すべての辺の長さが等しい』ひし形ですが、これらの定義とは対象的に対角線については長方形が 『対角線の長さが等しい』 、ひし形が 『対角線が直交する

中学校数学 証明のコツ 四角形の性質
ひし形の定理
ひし形の定理- 三平方の定理 ひし形 一辺の長さが19cmで、一方の対角線の長さが34cmのひし形がある。このひし形の面積を求めなさい。という問題です。自分では4cm2が答えだと思うのですが、確証が持てないので解説・確認をしてもらいたいです。どなたかお願いしますm(_ _)mひし形になる条件 対角線がそれぞれの中点で垂直に交わるとき、ひし形になる。(証明) 問題 1 平行四辺形abcdが、次の条件をもつと、それぞれ、どんな四角形になりますか。 解答) (2)ab=bc (




特別な平行四辺形 画質上 Youtube
平行軸の定理(復習) 重心 a m 重心を通る軸のまわ りの慣性モーメント i g それに平行な軸のま わりの慣性モーメント i i i ma 2 = g 工学院大学の学生のみ利用可:印刷不可:再配布不可(c)加藤一方でひし形では、すべての辺の長さが等しいものの、すべての角度が等しくなっている必要はありません。 ひし形の定義は「4つの辺の長さがすべて等しい」です。この定義から導き出される定理として、「 対角線が垂直に交わる 」があります。以下の証明:(三角形の外心及び、ひし形定理による) ひし形abdcで、線分ac上の垂直二等分線①の交点をpとする。 図の線分aqで、∠acqに線対称な∠arqを求め、 四角形arqc②とするとき、線分ct=cqなので 四角形trqcはひし形である③
ご意見・ご感想 V=h (S1S2√(S1×S2))/3, V:体積, h:高さ, S1:下底面積, S2:上底面積この公式で算出した数値と、少数以下が多少違いますが参考にどちらが正しいでしょうか例えば 上部から数センチ下がり時の容積を簡単に計算出来ないでしょうか?図形の定義及び性質〔参考:算数教科書の定義・定理辞典 著 志水廣 啓林館わくわく算数〕 図形 定義 性質 三角形 3本の直線で囲まれた図形 角が3つある。 角の総和は180°である。 四角形 4本の直線で囲まれた図形 角が4つある。ひし形の面積を求める公式は、s = (縦の対角線)×(横の対角線)÷2 で表されます。このページでは、ひし形の面積の求め方を、計算問題と共に説明しています。また、公式の導き方も説明しています。
ひし形 定義 定理 ひし形(菱形)とは?定義や面積の求め方(公式)、計算問題 ひし形(菱形)とは、 つの辺の長さがすべて等しい四角形 のことをいいます 定理 対角線がそれぞれ中点で垂直に交わる四角形はひし形である。バリニヨンの定理の例と解法 の バリニヨンの定理 四辺形で点が辺に連続して結合されている場合は、平行四辺形が生成されることを証明します。 この定理はPierre Varignonによって公式化され、1731年に出版されました。 数学の要素 「 この本の出版は彼の問題 下の図のひし形 \(abcd\) の \(4\) つの辺すべてに内接する円を、 定規とコンパスを用いて作図しなさい。 解説 円の作図なので、 円の中心と、半径を定めることが目標です。 完成図をラフスケッチ




ひし形の対角線の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



Http Ed City Daito Osaka Jp Weblog Files Tani Jhs Doc 7819 Pdf
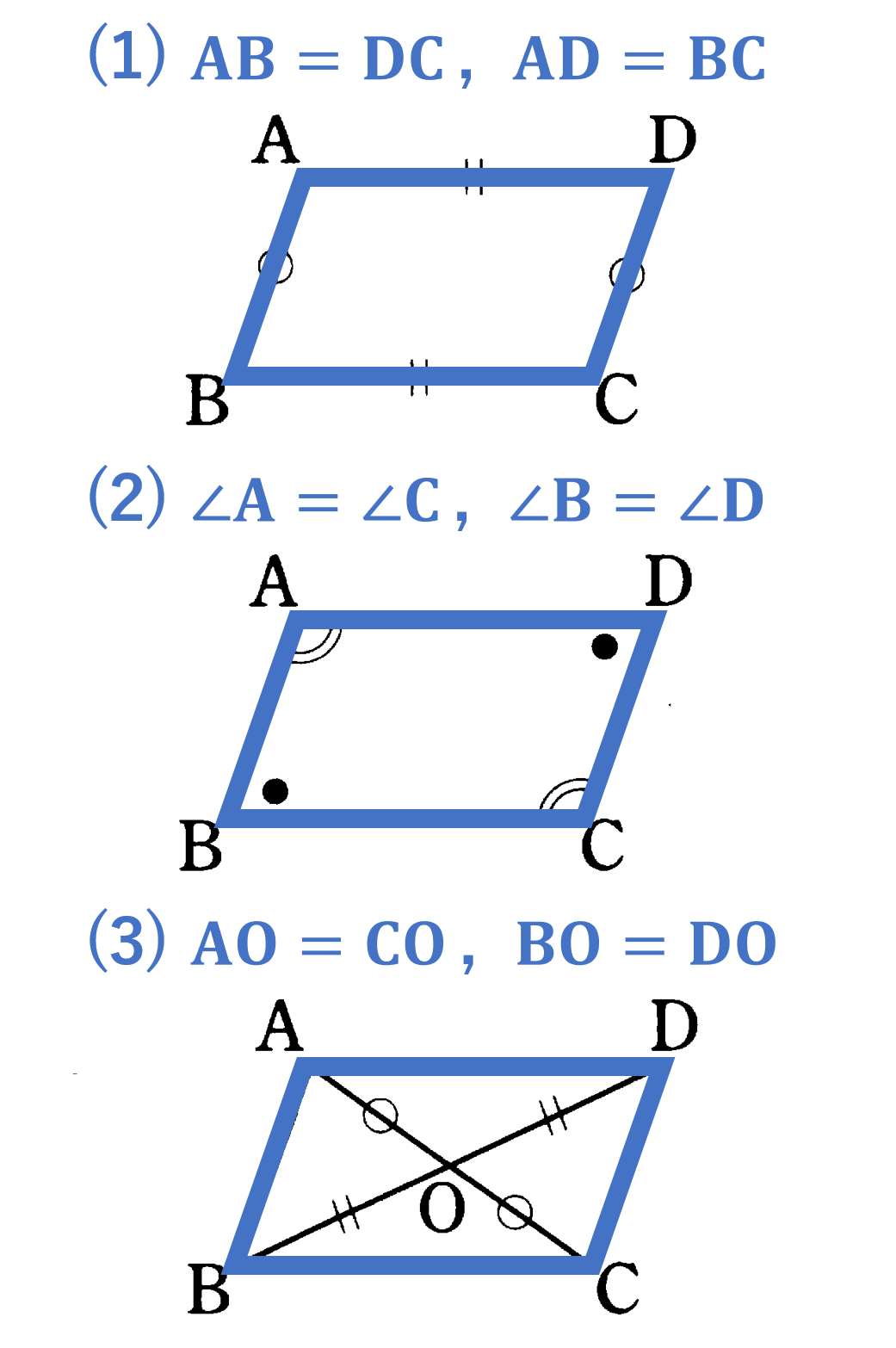
交流回路の計算には、キルヒホッフの法則、重ねの理あるいはテブナンの理が用いられる。 ここでは、具体回路例を用いて、それぞれの方法による解き方の違いや活用上の特徴などについて解説する。 関連講座 「回路定理、対称座標法による不平衡三相下の三平方の定理の証明の方法について,太郎さんと花子さんが考えています。あとの(1), (2)の各問いに答えなさい。 三平方の定理 直角三角形の直角をはさむ2辺の長さを a,b, 斜辺の長さをc とすると,次の関係が成り立つ。 a 2+ b = cひし形 対角線がそれぞれの中点で垂直に交わるときひし形になる。 それぞれの中点で交わるので四角形abcdは平行四辺形になる。 aobと cobと codと aodで 平行四辺形の性質より bo=bo=do=do 1 ao=co=co=ao 2 仮定(垂直に交わる)より よって




ひし形 菱形 の面積の公式は 対角線 対角線 2 見やすい図で即理解 高校生向け受験応援メディア 受験のミカタ




特別な平行四辺形 画質上 Youtube
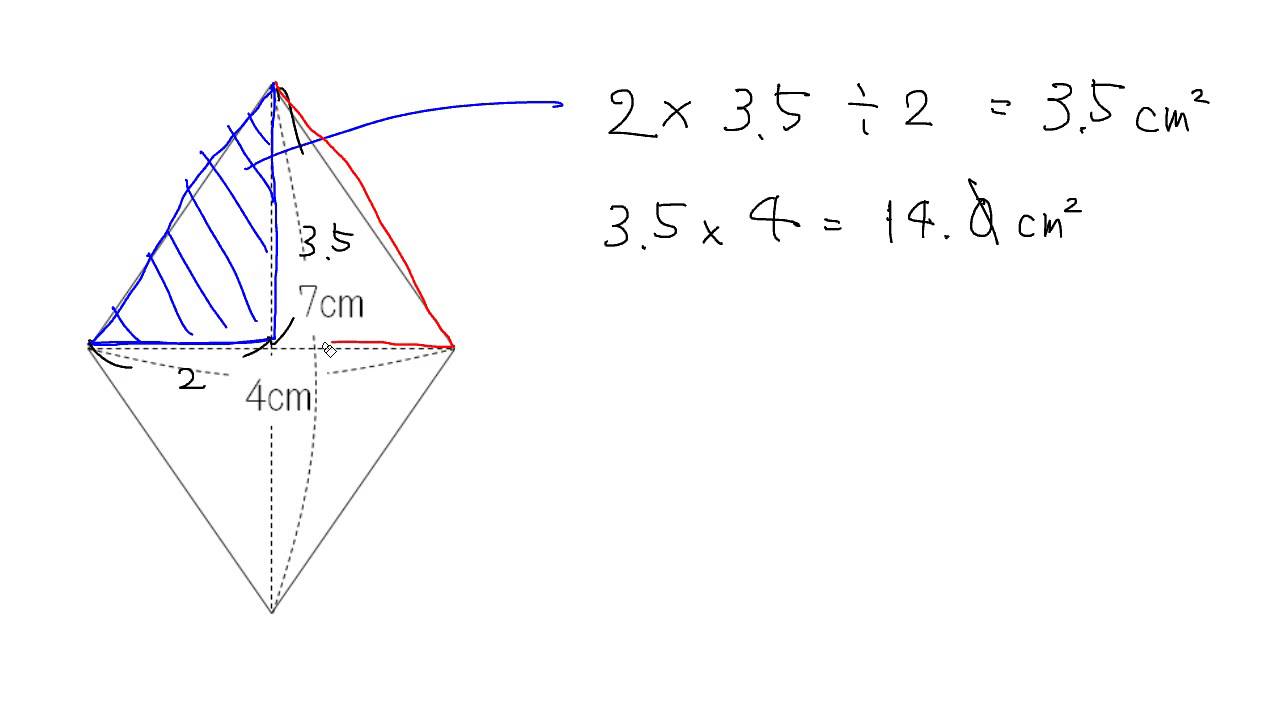
7章 三平方の定理 0 学習の基本 3 正多角形の面積 問題 次の図形の面積をそれぞれ求めよ。 ⑴ 1辺の長さが2cm の正六角形 ⑵ 1辺の長さが6cm の正八角形 解 ⑴右の図のように6つの正三角形に分けて考えると, 正三角形の高さは 㲋3 2 ×2=㲋3(cm) になるから,④ 逆は「四角形abcd で,対角線ac とbd が垂直に交わればひし形なる。」であるが,こ れは正しくない。 問題 次のそれぞれの下線部分の逆を書け。また,正しい場合は ,正しくない場合は×を書け。 (1) abc で,∠a=90°ならば∠b+∠c=90°である。定理 ひし形の対角線はそれぞれ中点で垂直に交わる。 定理 対角線がそれぞれ中点で垂直に交わる四角形はひし形である。 定理 隣り合う2辺の長さが等しい平行四辺形は 定 菱形(ひしがた、りょうけ



ひし形 菱形 とは 定義や面積の求め方 公式 計算問題 受験辞典
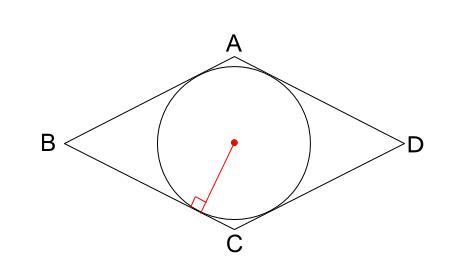



作図 ひし形の内接円 中学数学の無料オンライン学習サイトchu Su
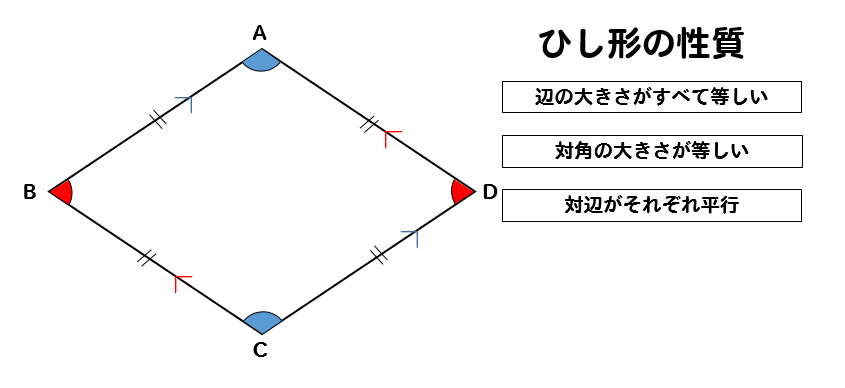
定理 ひし形の2組の向かい合う角の大きさはそれぞれ等しい。 定理 ひし形の対角線はそれぞれ中点で垂直に交わる。 定理 対角線がそれぞれ中点で垂直に交わる四角形はひし形である。 定理 隣り合う2辺の長さが等しい平行四辺形はひし形である。 定理長方形の定理の逆 四角形で対角線の長さが等しければ 長方形である × 長方形の定理の逆 ~平行四辺形で対角線の長さが等しければ 長方形である ひし形の定理の逆 四角形で対角線が垂直に交われば ひし形である × ひし形の定理の逆方を引き出すことができる。また、この課題学習を三平方の定理を学習した後に実施すれば、 (ウ)の対角線の長さを正確に求めることかできる。 三平方の定理を利用して、ひし形pbqdの面積を求める。 ap=ズ(cm)とする。 d bd2=122+ ゴ8 bd>0⊥車り bd



ひし形 菱形 とは 定義や面積の求め方 公式 計算問題 受験辞典




最高のコレクション ひし形 の 定理 シモネタ
ひし形の定義は 「4つの辺がすべて等しい四角形」 正方形の定義は 正方形の定理 「4つの角がすべて等しく、 「正方形の対角線は、 4つの辺がすべて等しい四角形」 長方形の定理 「長方形の対角線は、長さが等しい。」 ひし形の定理菱形(ひしがた、りょうけい)、斜方形(しゃほうけい、 rhombus )は、4本の辺の長さが全て等しい四角形である。 成立条件に、 隣り合う2辺の長さが等しい平行四辺形;中点連結定理を使った問題を解説! 相似の面積比を求める問題をイチからやってみよう! 面積比!平行四辺形の面積問題を解説! 面積比!台形の面積比問題を解説! 円錐の体積比を解説!



Www Tsumugi Ne Jp Member St2 54 Pdf




1 と 2 がなぜそうなるのか理由を教えていただきたいです Clear
ひし形の定理 定理 ひし形の2組の向かい合う角の大きさはそれぞれ等しい。 定理 ひし形の対角線はそれぞれ中点で垂直に交わる。 定理 対角線がそれぞれ中点で垂直に交わる四角形はひし形である。 定理 隣り合う2辺の長さが等しい平行四辺形は 定 菱形(ひしがた、りょうけい)、斜方形ひし形の定義から,対角線をひくことによって,合同な三角形ができることに着目し,それを証明することでひし形の定理としてまとめる。 (図4) 平行四辺形の特別な場合として包含関係にあることを捉える。 二等辺三角形中点連結定理を使った。 対角線に注目し、平行線の同位角・錯覚を使った。 四角形efgh がひし形になると予想していた人がいます。最初の四角形にどん な条件が加われば四角形efgh はひし形になるのかな? 対角線が関係してそう。




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun



菱形と長方形はどちらが美しいですか Quora
ひし形っていうのは、すべての辺が等しい四角形。 ということは、ちょっと見方を変えると 「2組の向かい合う辺がそれぞれ等しい」 ってことでもある。 つまり! ひし形は平行四辺形になるための条件を満たしているということが分かります。 このことから1 調和関数と等角写像 1 熱方程式 平面上の領域D に均質な物体があり、境界の温度が一定に保たれているとする。 そし て、領域D 内には熱源はないものとする。 このとき、D 内の点(x,y) での時刻t におけ る温度H(x,y,t) は次の形の偏微分方程式 (1) ∂H ∂t = H を満たすことが知られている。図形 定義・定理 まとめ 対頂角 𝟖は等しい 直線の角度 ° 平行線の 同位角 𝟖 は等しい 角形の内角の和 °×(𝒏− ) 平行線の 多角形の外角の和錯角 𝟔は等しい ° 同位角 が等しければ、2直線は平行 〇 合同な図形の対応する線分や角は等し



Http Mathaca Com Download 2 12kaisetu Pdf



Http Ed City Daito Osaka Jp Weblog Files Tani Jhs Doc 7819 Pdf
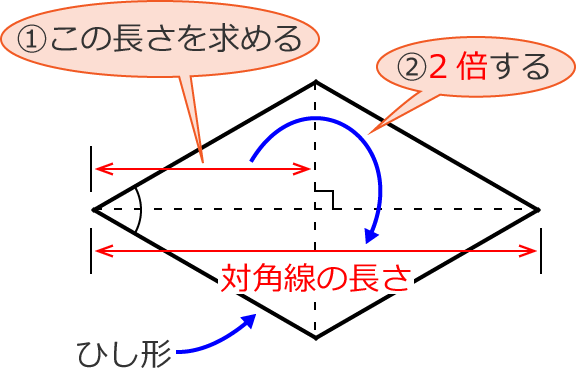
ひし形の面積を求める公式は ひし形の面積 対角線 対角線 ひ し 形 の 面 積 = 対 角 線 × 対 角 線 ÷ 2 なので、 ひし形の面積 ひ し 形 の 面 積 = 8 × 4 ÷ 2 = 32 ÷ 2 = 16 ( c m 2) になります。 次は小数点を含むひし形の面積を計算します。中点連結定理1 問題1 右の ABC において, AB , BC , CA の中点をそれぞれ P , Q , R とし,辺の長さをそれぞれ AB=8 , BC=10 , CA=6 とするとき,次の辺の長さを求めなさい. __________PQ= __________QR= __________RP= 採点する やり直す ヘルプ ABC において AB,BC の中点が
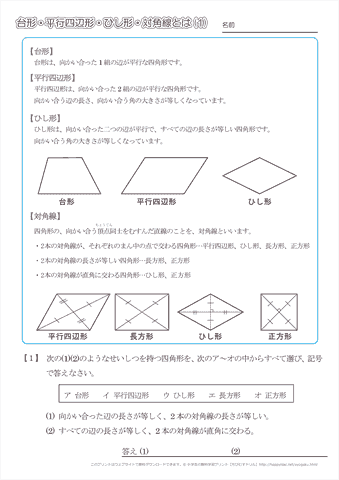



小学4年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生



Q Tbn And9gctygkghqwdw3gq3qrgj51pa5x3j74rgia9vkgwdewbxneabh7zq Usqp Cau



ひし形 菱形 とは 定義や面積の求め方 公式 計算問題 受験辞典
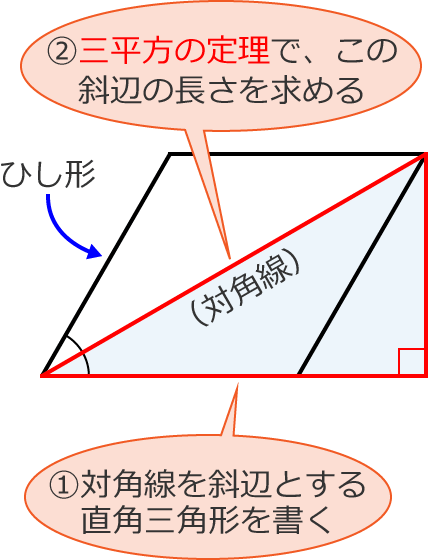



ひし形の対角線の長さの求め方



Www Tsumugi Ne Jp Member Data Sm2 5 Sm2 5 4 Pdf



ひし形 菱形 とは 定義や面積の求め方 公式 計算問題 受験辞典




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット
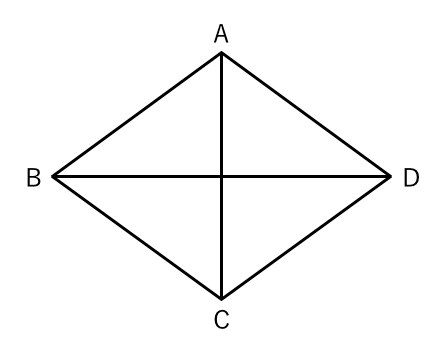



ひし形についての問題 苦手な数学を簡単に
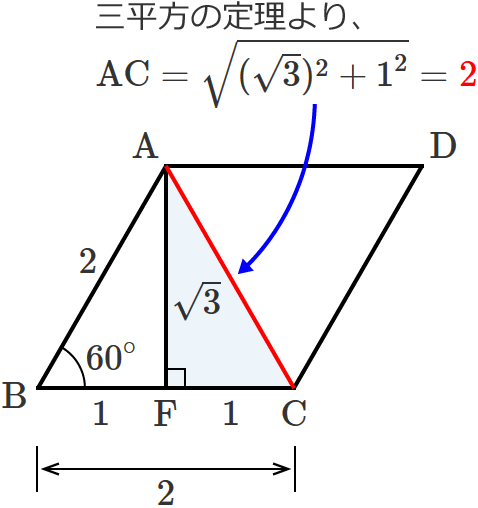



ひし形の対角線の長さの求め方



最高のコレクション ひし形 の 定理 シモネタ



ひし形に内接している円なんですけど 一辺の長さlのひし形があり 直径の Yahoo 知恵袋
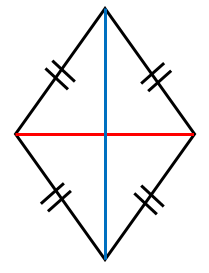



ひし形の面積を求める方法と例題 具体例で学ぶ数学
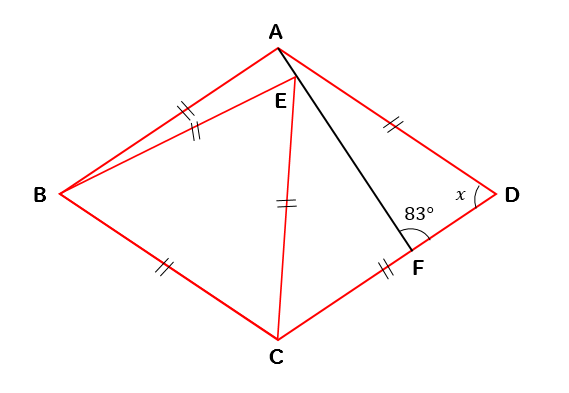



正三角形の角度 正方形 ひし形との融合問題を解説 数スタ



最高のコレクション ひし形 の 定理 シモネタ




ひし形の面積の求め方 公式と計算例



3




ひし形の面積の求め方 公式と計算例



ひし形 菱形 とは 定義や面積の求め方 公式 計算問題 受験辞典




中3 中点連結定理の証明です やり方も教えてください Clear




3分でわかる ひし形 菱形 の定義 Qikeru 学びを楽しくわかりやすく
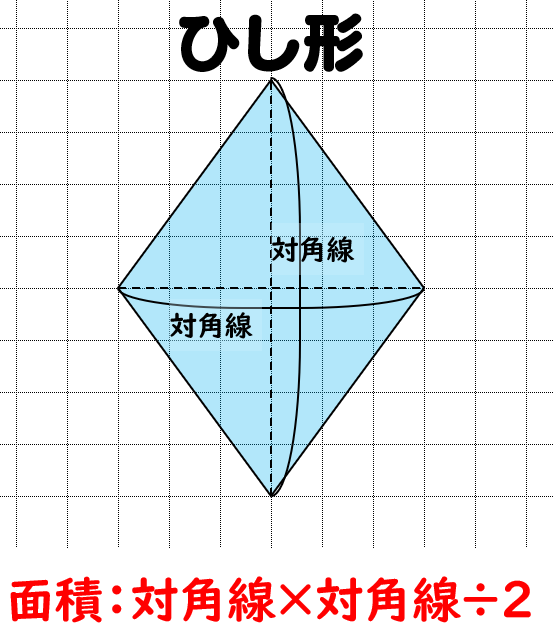



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun




3分でわかる ひし形 菱形 の定義 Qikeru 学びを楽しくわかりやすく



1



高校入試 英語 数学 学習 三角形と四角形 特別な平行四辺形



最高のコレクション ひし形 の 定理 シモネタ



正三角形の角度 正方形 ひし形との融合問題を解説 数スタ




平行四辺形の辺や角を求める Youtube




ひし形の面積の求め方 公式と計算例



中学数学 平面図形



ひし形の対角線の長さの求め方



高校入試 英語 数学 学習 三角形と四角形 特別な平行四辺形



数学の質問です台形 長方形 ひし形 正方形の定理 定義を教えてください Yahoo 知恵袋




ひし形の対角線の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
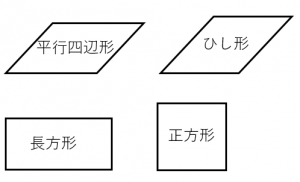



平行四辺形 ひし形 長方形 正方形の違い 具体例で学ぶ数学



長方形 ひし形 円 等脚台形 直角三角形 正方形 の定理と定理を教えてくだ Yahoo 知恵袋




平行四辺形の定義 定理 性質 と証明問題 中学数学の図形 リョースケ大学




中学校数学 証明のコツ 年01月




ひし形の定義 性質 条件 Youtube
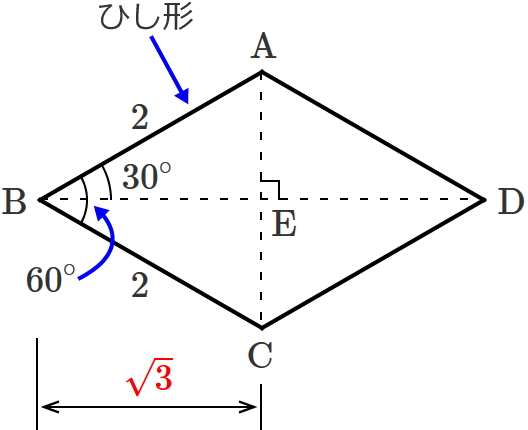



ひし形の対角線の長さの求め方




中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット




中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット
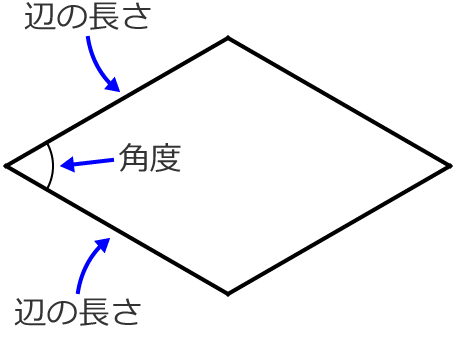



ひし形の対角線の長さの求め方




ひし形の対角線の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




ひし形の性質 対角線はなぜ垂直に交わるのか Qikeru 学びを楽しくわかりやすく



1




この問題の3番のoiを求める問題で 答えにあるひし形がどういう図形になるかわかりませ Clear
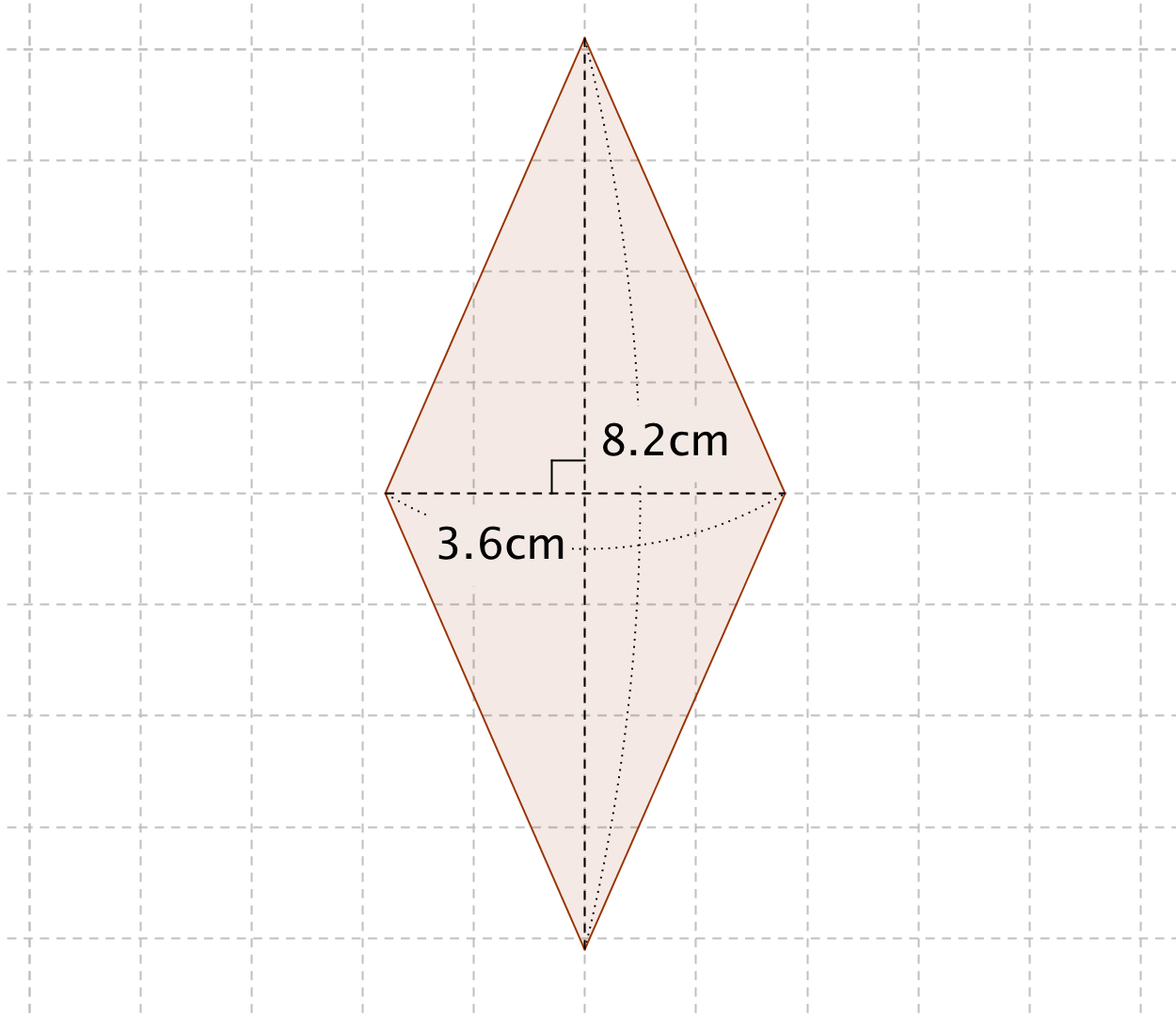



ひし形の面積の公式 算数の公式




中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット



ひし形の面積の公式 Youtube



四角形の4つの辺の中点を結んでできる四角形



ひし形の定理全部教えてくださいm M 対角線が互いに二等 Yahoo 知恵袋




数学 中2 76 長方形 ひし形 正方形 Youtube
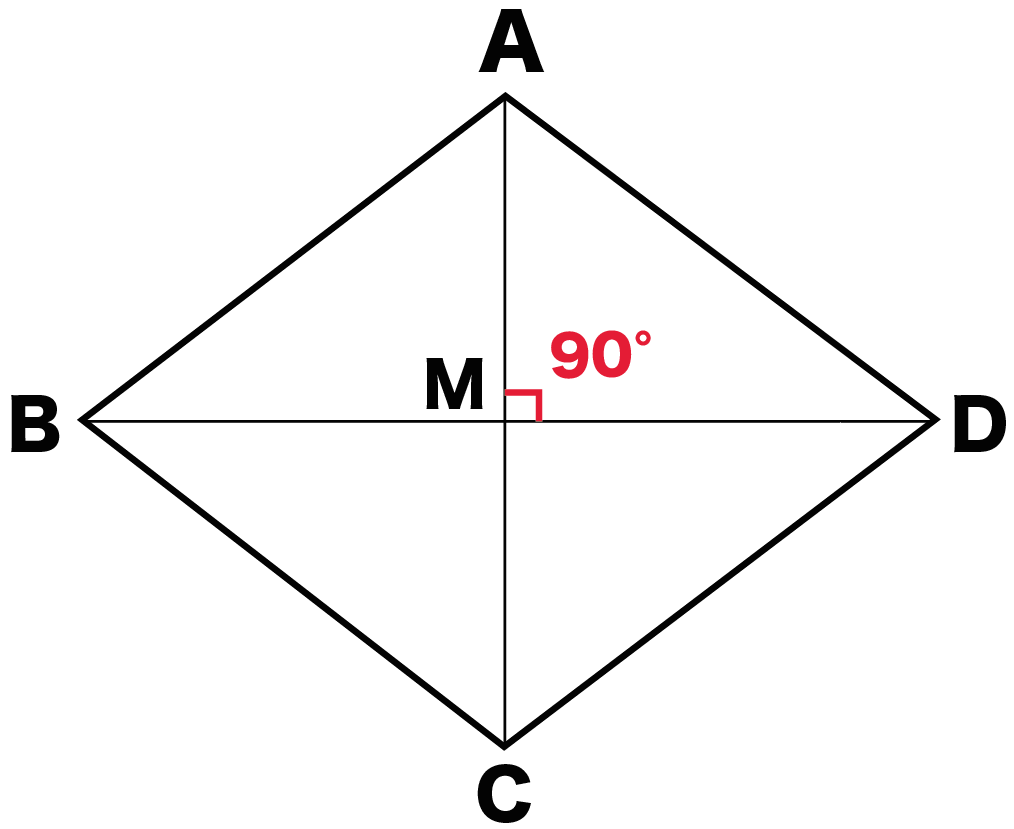



ひし形の性質 対角線はなぜ垂直に交わるのか Qikeru 学びを楽しくわかりやすく




菱形 Wikipedia
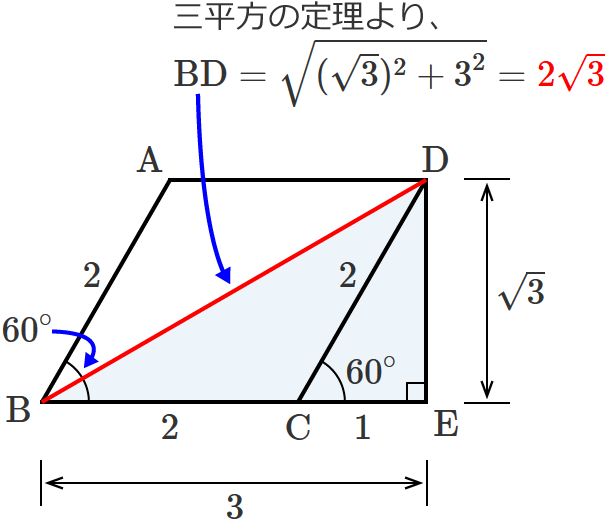



ひし形の対角線の長さの求め方
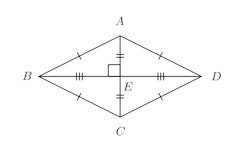



ねこ騙し数学




S Abcdad Ac pq R S Descubre Como Resolverlo En Qanda
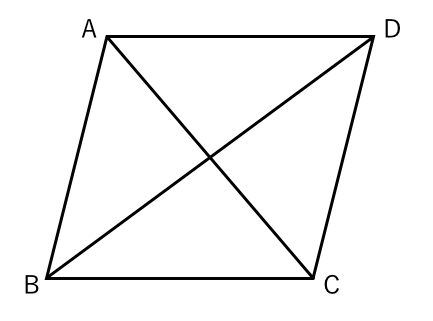



ひし形についての問題 苦手な数学を簡単に




中学校数学 証明のコツ 四角形の性質




中点連結定理の利用で 以下の図形の中点を結ぶとどんな四角形ができるか またその証明を Clear
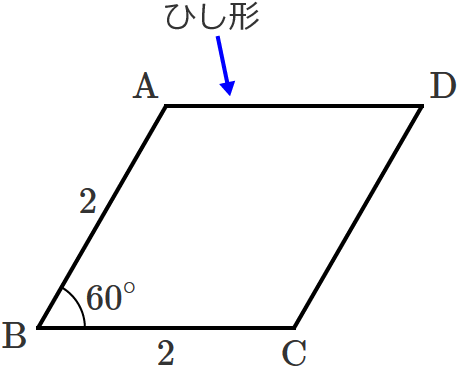



ひし形の対角線の長さの求め方



ひし形 菱形 とは 定義や面積の求め方 公式 計算問題 受験辞典



Http Ed City Daito Osaka Jp Weblog Files Tani Jhs Doc 7819 Pdf



高校入試 英語 数学 学習 三角形と四角形 特別な平行四辺形
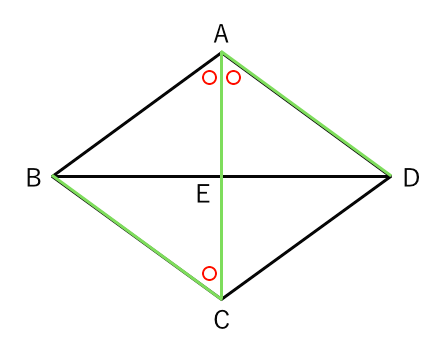



ひし形についての問題 苦手な数学を簡単に




中学数学 特別な平行四辺形について Clear




中点連結定理の利用で 以下の図形の中点を結ぶとどんな四角形ができるか またその証明を Clear
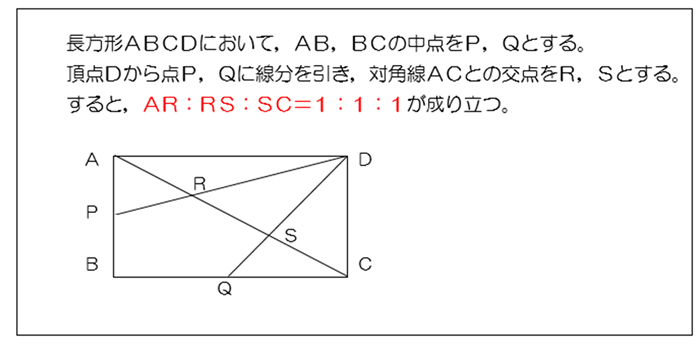



授業実践記録 数学 新しい 定理 とその活用 啓林館




すど ベクトルがいかに 無慈悲なる初等幾何定理自動証明マシーン であるかを紹介するために私がよく使う例です



高校入試 英語 数学 学習 三角形と四角形 特別な平行四辺形
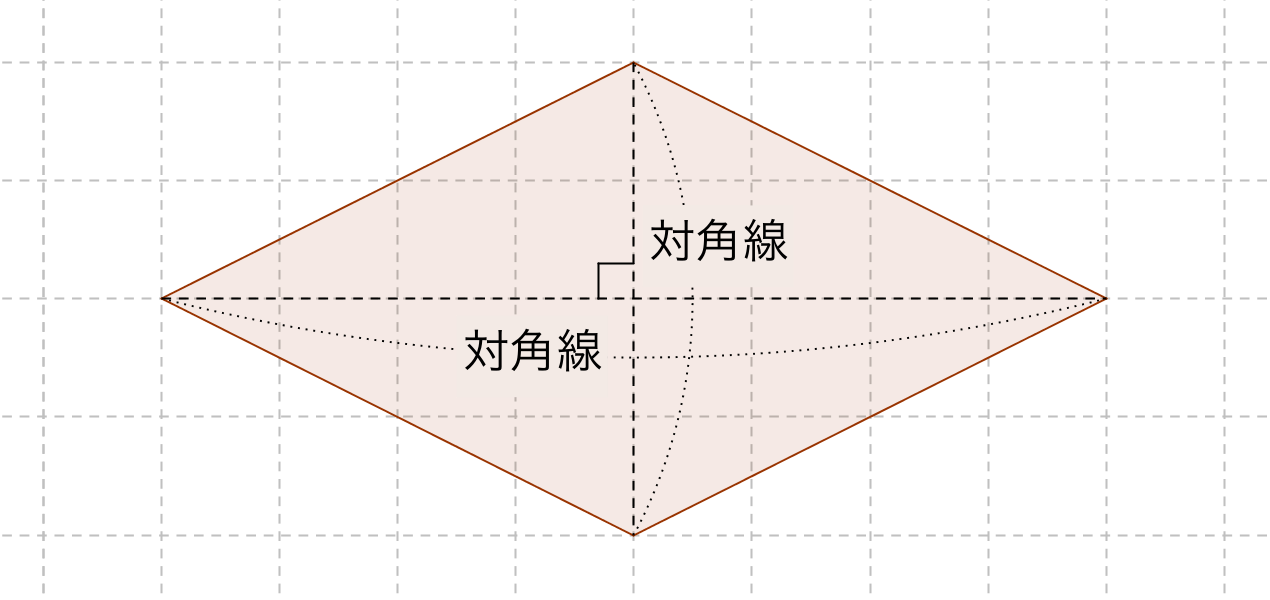



ひし形の面積の公式 算数の公式




3分でわかる ひし形 菱形 の定義 Qikeru 学びを楽しくわかりやすく



Http Ed City Daito Osaka Jp Weblog Files Tani Jhs Doc 7819 Pdf




ひし形 菱形 の面積の公式は 対角線 対角線 2 見やすい図で即理解 高校生向け受験応援メディア 受験のミカタ




ひし形の面積の求め方 公式と計算例
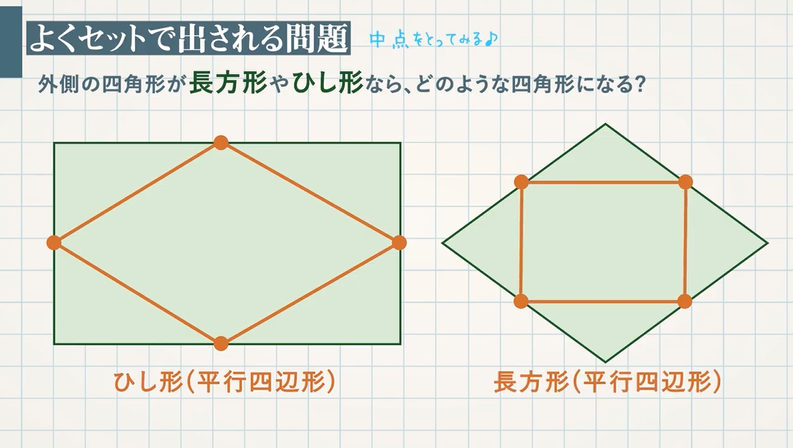



中点連結定理を使った平行四辺形であることの証明 教遊者
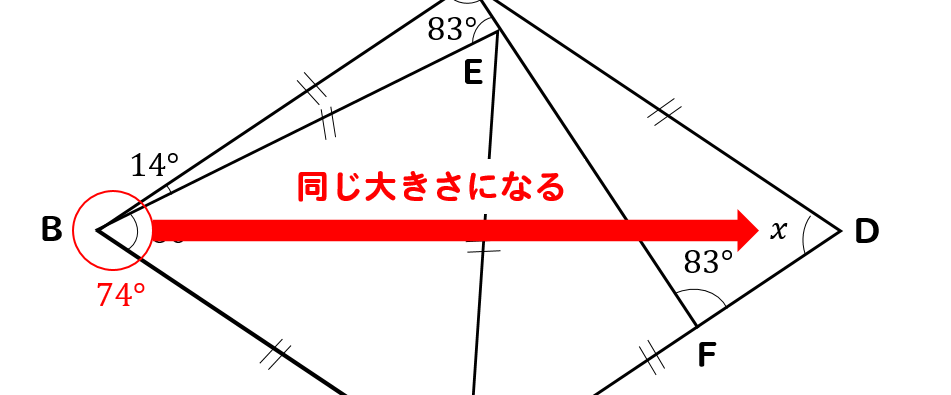



正三角形の角度 正方形 ひし形との融合問題を解説 数スタ




ひし形 菱形 の面積の公式は 対角線 対角線 2 見やすい図で即理解 高校生向け受験応援メディア 受験のミカタ




ひし形の対角線の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中学校数学 証明のコツ 年01月




中2数学 長方形 ひし形 正方形 映像授業のtry It トライイット



Http Www Edu City Misato Lg Jp Secure 0526teigi Teiri Kotae Pdf
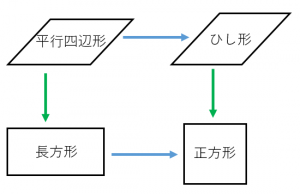



平行四辺形 ひし形 長方形 正方形の違い 具体例で学ぶ数学




3分でわかる ひし形 菱形 の定義 Qikeru 学びを楽しくわかりやすく



四角形efghがひし形や長方形になるときはどんなときか というレ Yahoo 知恵袋
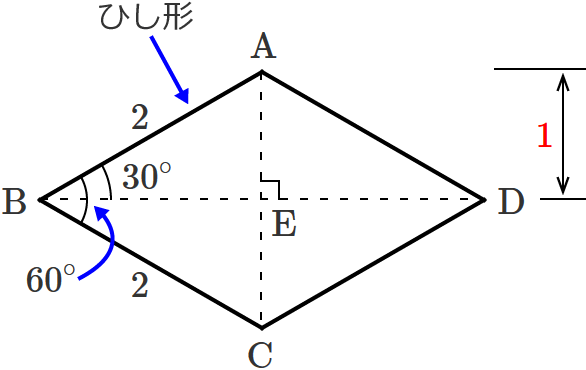



ひし形の対角線の長さの求め方




証明 1 教えてください 中点連結定理使うのはわかるのですが Clear
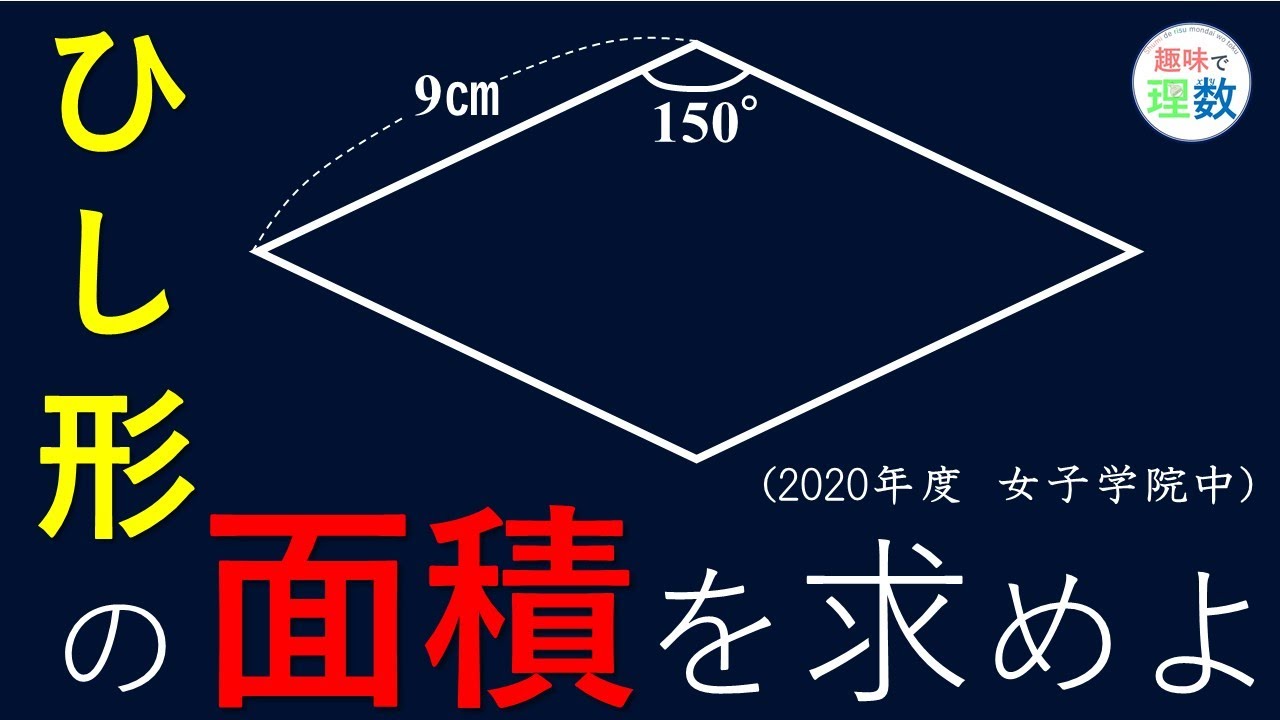



受験テクニック ひし形の面積は何 ですか Youtube
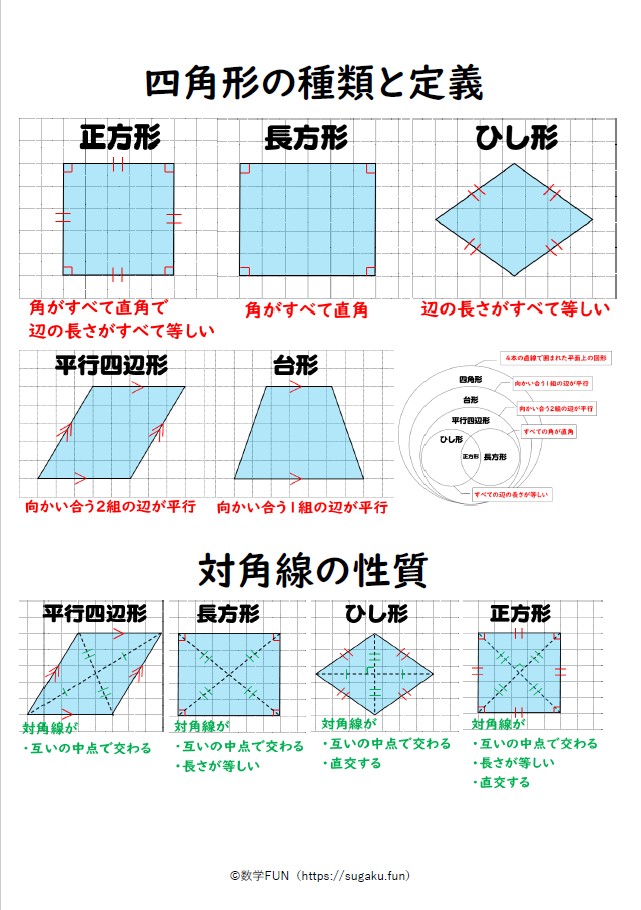



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun



2



0 件のコメント:
コメントを投稿