男子が少なくとも1人含まれる選び方の総数は、「8人の中から3人を選ぶ選び方の総数」から「8人の中から3人を選んだ際に男子が1人も選ばれない選び方の総数」から求められる。 8人の中から3人を選ぶ選び方は、 8 C 3 = 8 ⋅ 7 ⋅ 6 1 ⋅ 2 ⋅ 3 = 56 より、56通り。 また、「男子が1人も選ばれない選び方」というのは、「全員女子を選ぶ選び方」と言い換えられる組合せ ゲームのアイテムに69種類の効果のうち3つがランダムでつくというものがあり、自分が欲しい効果2つが同時についたアイテムが出る確率を計算しました。 どのくらい探し続ければ希望のアイテムが手に入るかわからないと絶望感がありますが、計算して確率がわかるとがぜんやる気が出ます。 一日に個ずつ拾えば平均2か月くらいで出るようなので頑張って※ この公式は,全部使う場合 の ※ もちろん, b の行き先の番号札3個をもらう方法の数 5 C 3 で計算しても同じになる. 5 C 3 = =10 《問題》 正しいものを選んでください. 選択肢をクリックすれば採点結果と解説が出ます.暗算では無理ですから計算用紙で計算してから答えてください. ≪1

この問題で場合の数を計算する時に なぜさいころの目が出る順番まで考慮しなきゃいけない Clear
場合の数 組み合わせ 公式
場合の数 組み合わせ 公式-例えば,順列では, (A,B)と (B,A)は違うものになりますが,組み合わせでは同じものを表していることになります。 数学的には,4個のものから3個取り出して並べる順列の数は, 4 P 3 =4×3×2=24となります。場合の数 基本公式 (重複or 重複しない) & (順列or 組合せ) 1 導入 重複組合せの使い方がよくわからないということはないだろうか 場合の数の基本公式において不思議なことがないだろうか 順列の公式nPr は異なるn 個のものからr 個を選んで並べるときに使う 例えば, 1,2,3 から2 つ選んで並べる




場合の数 並べる と 選ぶ の計算方法の違い
順列、組み合わせ、円、重複、組分け。これらの場合の数の違いとその見分け方を簡単に解説します。 ここでは共通の例として、7個のガラス玉があった場合を考えてみます。 順列 7個のガラス玉から3個選んで一列に並べる $_7p_3$ 組み合わせ 場合の数と確率 場合の数と確率を総まとめ! 各種公式重要記事一覧 21年2月19日 場合の数と確率に関するさまざまな公式をまとめていきます。 詳細記事へのリンクも載せていますので、気になる問題や解き方があればぜひ参考にしてくださいね公式としては、 異なるn個から同じものを選ぶことを許して、r個選ぶ場合の数は、 で済んで(済ませて)しまうが、具体例での説明からこの公式への結びつきがしにくく、演習問題になると使い方さえ分からなくなってしまう。 教科書の扱いもしたがってずいぶん苦労しているようで今回の
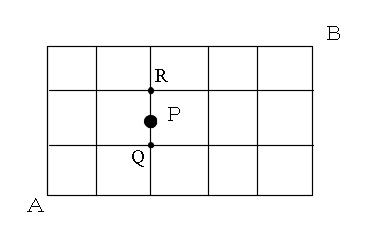
場合の数2| 順列のnPrの考え方と公式は超カンタン! 「場合の数」は樹形図を考えるのが最も基本的で,樹形図から 和の法則と 積の法則は簡単に説明できることを前回の記事で解説しました. 積の法則の最も簡単な応用は 順列 です. 「モノを一列に並べること」を順列といい,「 n 個のものから r 個選んで並べる場合の数」を n P r で表します. 「順列 解答 「→四つと↑三つを一列に並べたもの」と「最短経路」は一対一に対応する。 よって「→四つと↑三つを一列に並べたもの」の数を数えればよい。 そのような場合の数は同じものを含む順列の公式より \dfrac {7!} {4!3!}=35 4!3!7!Top spi非言語 場合の数 問題6(コインの裏表) 今回はじめて タグ青 タグ黄 タグ赤 タグ白 3 分 制限時間 1 00 非表示 表示 問題 コインを6回連続で投げる。このとき、表が4回出るような表裏の出方は何通りか。 選択肢をクリックすると、採点して解答を表示します。 a 6通り b 9通り c 12
場合の数の問題は大まかに分けると 順列 と 組み合わせ があり,これらは掛け算と割り算を駆使することで求めることができます. では実際に解いてみましょう! 1a,b,cの3人を1列に並べる方法は何通りあるか. *1 解答1 書き出す解き方 書き出すときは必ず 辞書順 に! $$\rm (abc), (acb 例えば、1, 2, 3の三つの数字について、順列の全ての場合を列挙すると次の6通りがあります。 組み合わせでは、上記6つを全て同じものとみなします。 つまり、順列における並び順のパターンを入れ替えたときに、同じ順番になるものはそれを1通りとみなさず、1, 2, 3の三つの数字の組み合わせは、 の1通りのみとなります。 順列 によって並べられた 個の場合の数と確率 組み合わせCの公式と使い方を徹底解説! 5分でサクッと解説! 21年4月22日 「組み合わせがよくわからない」 「順列との違いがわからない」 今回はこんな悩みを解決します。 高校生 組み合わせのときはCを使うことは分かるけど、問題が解けません
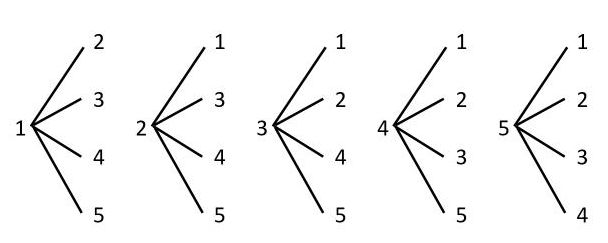



何通りあるかを計算で求めよう 場合の数 が苦手な小学生のための公式の使い方 中学受験ナビ
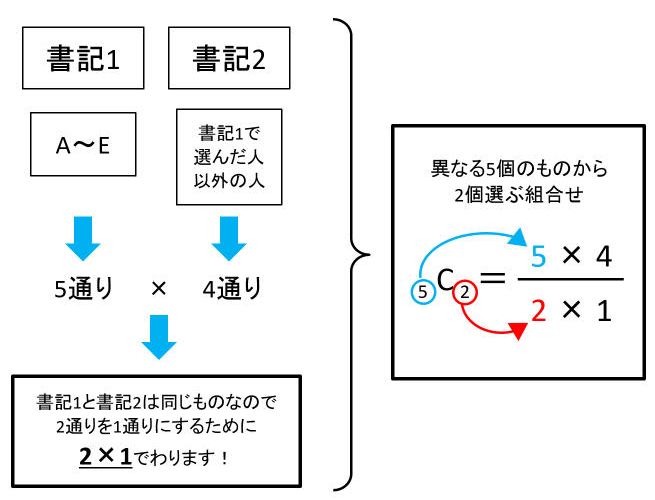



何通りあるかを計算で求めよう 場合の数 が苦手な小学生のための公式の使い方 ページ 2 2 中学受験ナビ
では、この公式を参考にして 100までの自然数のうち、2または3の倍数は何個あるか? の答えを求めよう。 100までの自然数のうちの、2の倍数の集合をAとして、3の倍数の集合をBとすると n(A)= 100/2 =50 なので、集合Aの要素の個数(2の倍数の個数)は 50個、つまり n(A)= 50 である。 n(B)について 青,赤,黒の3種類から重複を許して4個選ぶ場合の数なので,重複組合せの公式 n r − 1 C r {}_{nr1}\mathrm{C}_r n r − 1 C r で n = 3, r = 4 n=3,r=4 n = 3, r = 4 とすればよい。場合の数・順列組み合わせの公式 場合の数の和の法則 A、Bという2つ同時には起こらない事象がある。Aの起こり方がm通り、Bの起こり方がn通りあるとき、AまたはBの起こる場合の数は、m+n通り 場合の数の積の法則 A、Bという2つの事




組み合わせの総数 場合の数 理数系無料オンライン学習 Kori




場合の数 は 順列 の計算の応用 中学受験プロ講師ブログ
組み合わせとは 組み合わせは順列と混同されがちですが、その内容は大きく違います。それは 並べるのか並べないのか という違いです。どういうことかというと、例えば 5 人から 3 人を選ぶ のと 5 人から 3 人を選んで並べる ことは場合の数が場合の数6|「重複組み合わせ」は2パターンでok! 場合の数7|二項定理を理解しよう!場合の数を使って導出! 順列の公式を憶えること自体はそこまで難しくないと思われます。ポイントは、公式をいかに使いこなすか?ということです。そのならべ方・組み合わせの問題の違い 小学校で習う「場合の数」では主に 『ならべ方(順列)』 の問題と 『組み合わせ』 の問題があります。 これらは似たような問題ですが、解き方が異なるのでまずは見分けがつかないと解くことができません。




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun
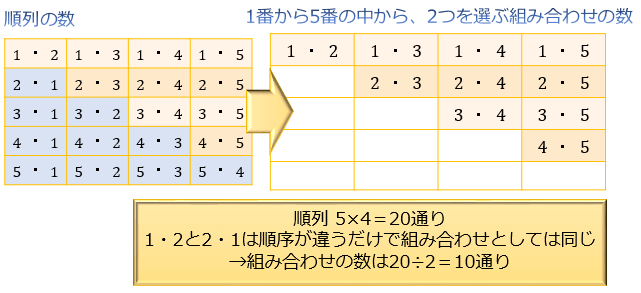



順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ
このような問題は「場合の数」と呼ばれ、「 4 p 2 」で計算するか、「 4 c 2 」で計算するかで大きく異なる答えを導きます。 そこで今回は、順列と組み合わせの違いを解説し、場合の数の単元において多くの方を悩ませる、 「積の法則」と「和の法則」の考え方の違い をご紹介します。という基本の公式がある。 解答 1通り 例題3 a、b、c、d、eの5人から3人を選ぶとき、選び方は全部で何通りありますか。 解説 下の公式より、 5×4×3 3×2×1 =10通り a-bとb-aを1通りとする場合を組み合わせという。 n個の中からm個を選ぶ選び方は という基本の公式がある。 解答 10通り 正解は、組み合わせの数の公式。 答えは 5 C 2 =10通りとなります。 この性質から、組み合わせの数は「コインを5回投げたときに2回表が出る 確率 」を求めるときなどに、 二項分布 の確率関数で利用されています。




場合の数 は 順列 の計算の応用 中学受験プロ講師ブログ




重複組合せはなぜ仕切りを使うの 整数解の個数を求める問題で鍛えよう 遊ぶ数学
n P r = n × ( n − 1) × ⋯ ( n − r 1) と書くことにしたわけです。 難しくありませんね。 例えば 6 個から 4 個を取って並び替える場合 6 P 4 = 6 × 5 × 4 × 3 = 360 と計算できることになります。 便利ですねー。 選ぶ分だけ 6 から 1 ずつ減らして掛け算するだけです。 じゃあ選ばないで全てを並び替えるなら数学切り抜き帳 異なる n 個のものから重複を許して r 個のものを取り出す場合の数 n H r は,公式 n H r = nr1 C r によって求められる。 この公式を説明しよう. 自動販売機による説明 次のようなジュースの販売機があるとする.《公式にする方法》 上の答は =56 ですが,しばしば登場するものに,毎回図を書くのは大変なので,通常 n C r への読み替え公式を利用します 5はボールの数(r)です3は子供の数(n)1です したがって,この結果は と表すことができます
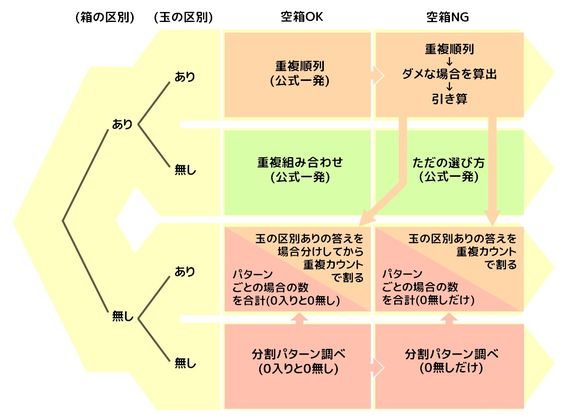



組み分け 部屋分け 問題全8パターンと解き方 数a 場合の数確率 そうちゃ S 図解英数ゼミナール



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b
前回 https//wwwyoutubecom/watch?v=tpOLtMx_Bfk 次回 https//wwwyoutubecom/watch?v=pq3pJVNZrIU&index=15&list=PLKRhhk0lEyzPV58dAXzmfZle_wg03CLhl場合の数とは、 ある事柄の起こりうる場合の総数 を指します。 サイコロの目の出方は何通りありますか? トランプの組み合わせは何通りありますか? このように 「全部で何通り? 」 を考えるのが場合の数です。 2つの事象によっては同時に起こらそんな、あなたのための「場合の数」専用 About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features
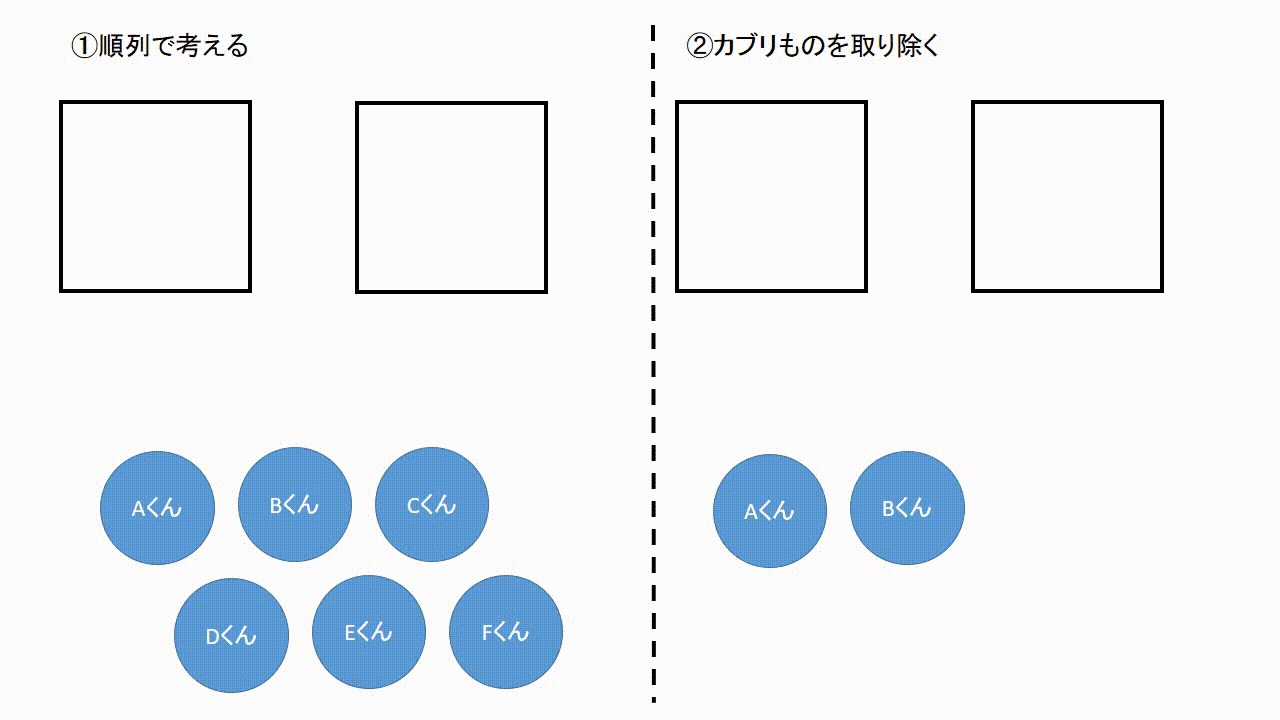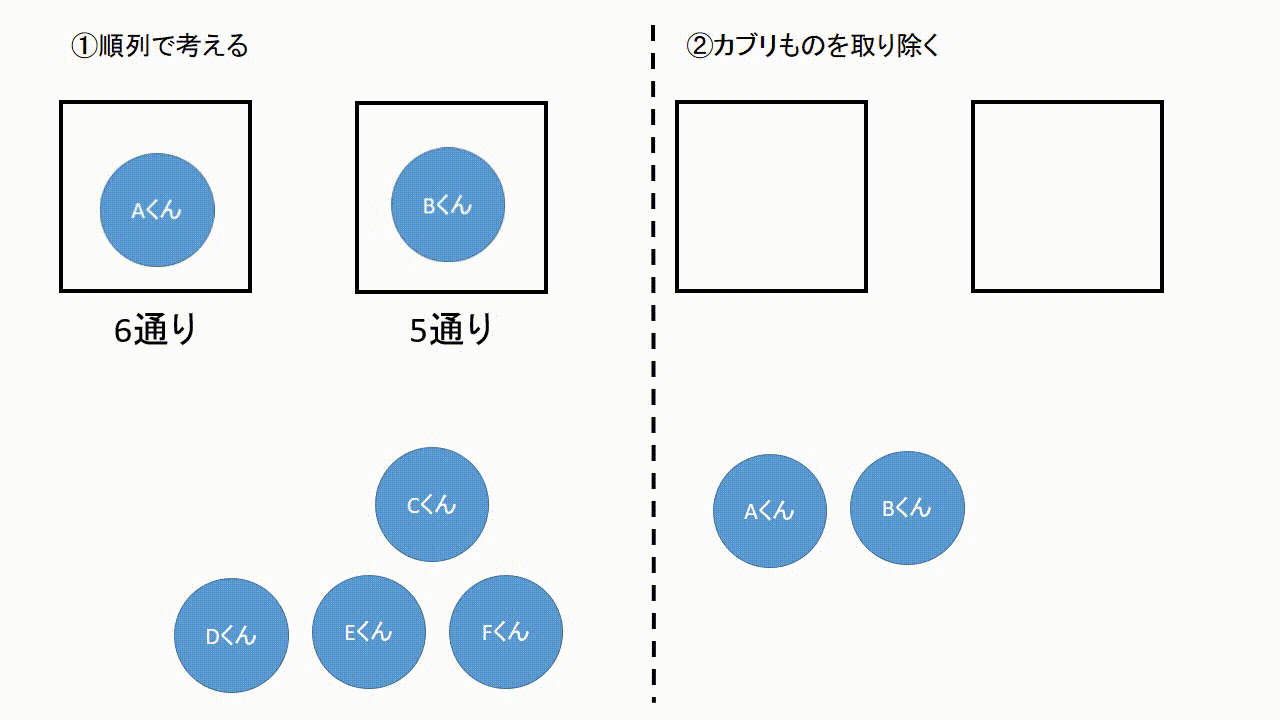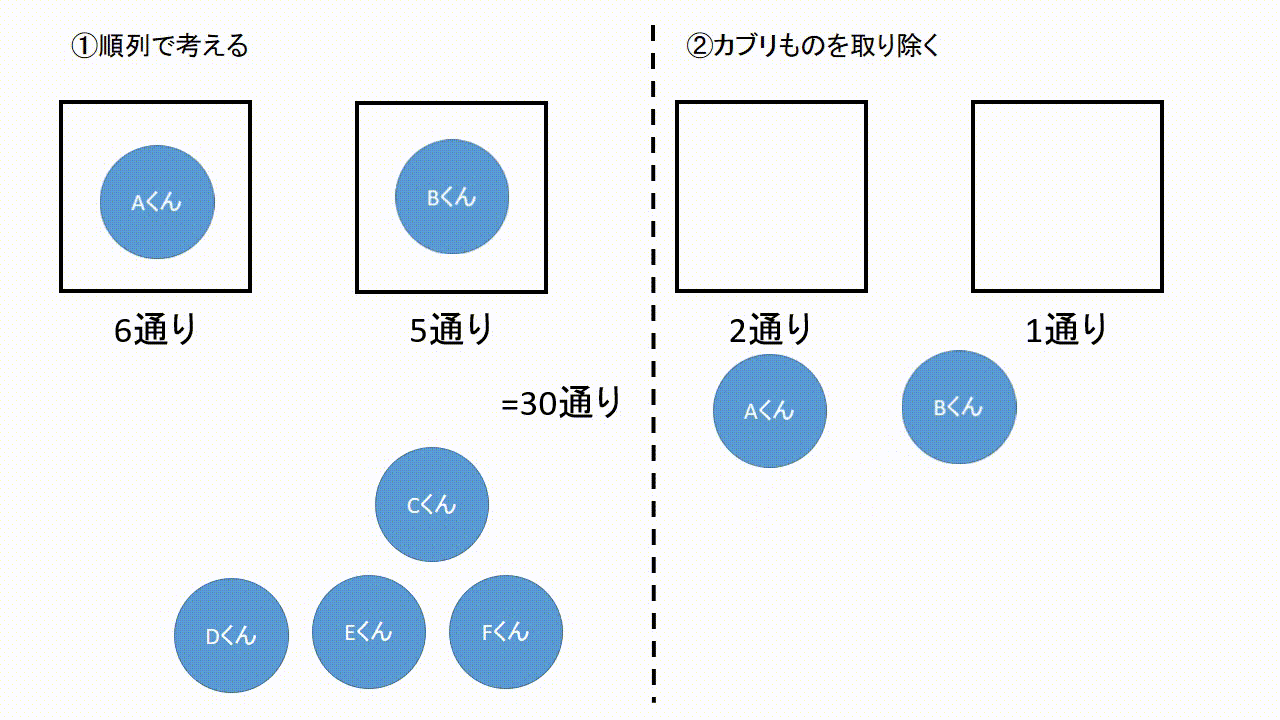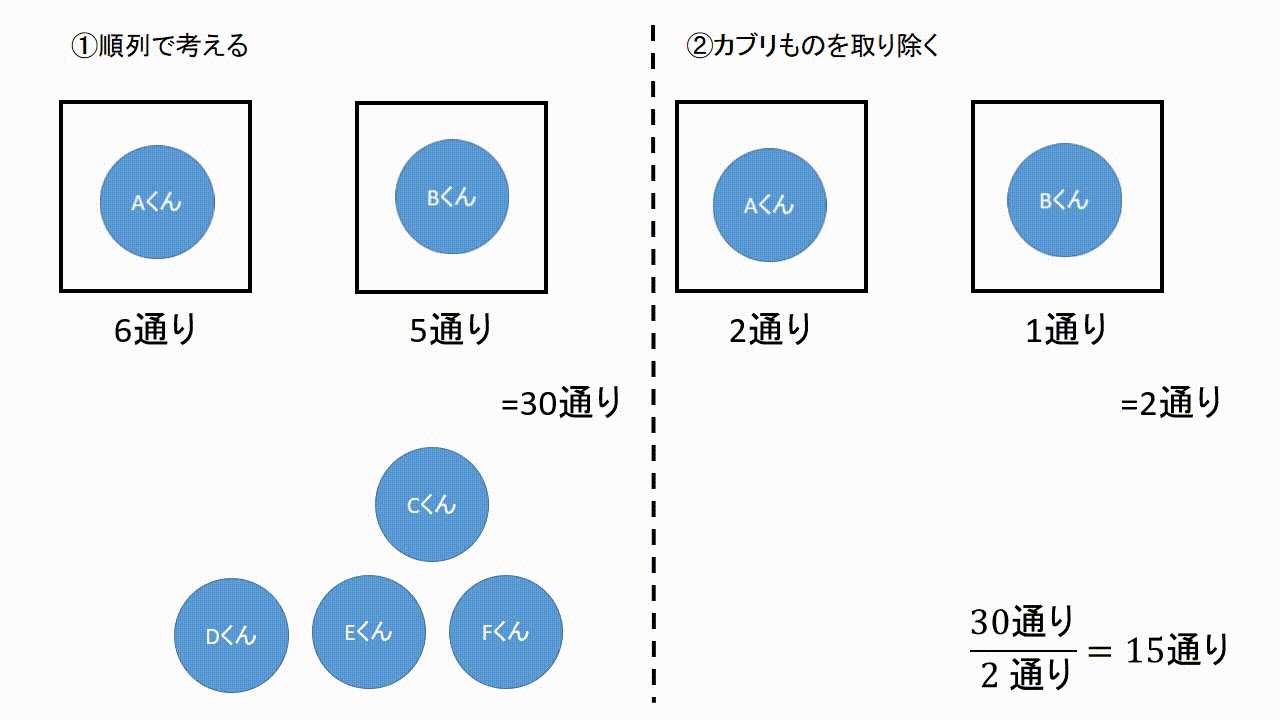



数学 確率を極めるには 場合の数 を極めろ




順列と組み合わせの公式とその違い 問題付き 理系ラボ




高校数学a 組合せの活用4 少なくとも 練習編 映像授業のtry It トライイット




確率の問題の解き方 場合の数 組み合わせ と確率 現役塾講師のわかりやすい中学数学の解き方




場合の数 順列 と 組合せ の 違いを例題付きで解説します




場合の数 順列組み合わせの公式一覧 数学a By となりがトトロ マナペディア




順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学



組み合わせの考え方と公式 組み分けと道順を求める問題の解き方




苦手な人向け 組み合わせcの計算のやり方を簡単にサクッと解説するぞ 数スタ
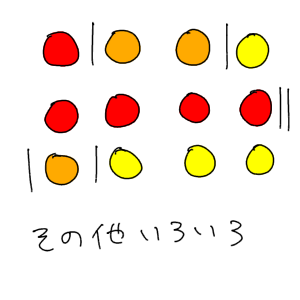



重複組み合わせは絵を描けば理解できる イラストで解説 理数白書




5講 組合わせ 1章 場合の数と確率 問題集 高校数学a




この問題で場合の数を計算する時に なぜさいころの目が出る順番まで考慮しなきゃいけない Clear




小学6年生の算数 場合の数 組み合わせ 練習問題プリント ちびむすドリル 小学生




高校数学a 重複組合せ Nhr 受験の月
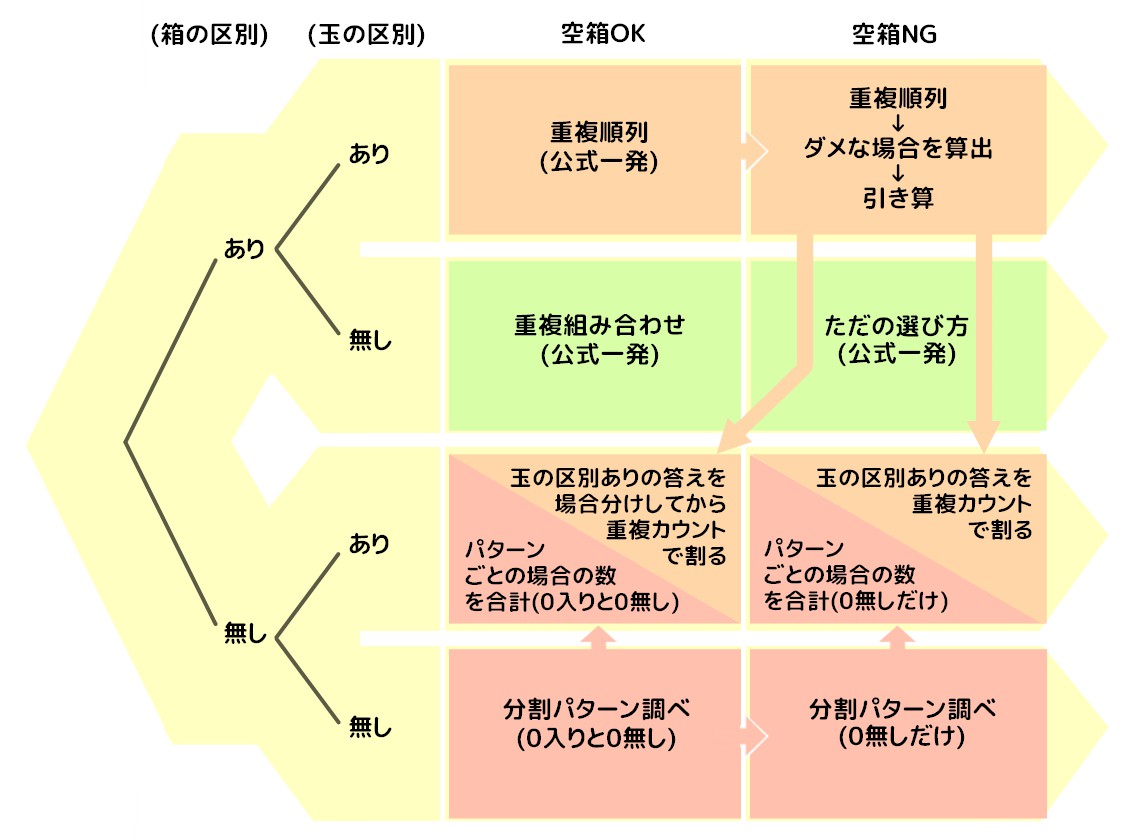



場合の数 確率の総合案内 定理 公式の総まとめと復習 そうちゃ S 図解英数ゼミナール




場合の数 順列は2時間で解けるようになる 外資系コンサルタントが主夫になったら




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




場合の数19 円順列と数珠順列 怜悧玲瓏 高校数学を天空から俯瞰する
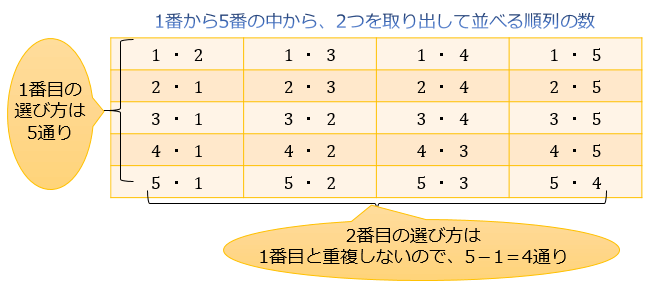



順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




場合の数 並べる と 選ぶ の計算方法の違い




小学6年生の算数 場合の数 組み合わせ 練習問題プリント ちびむすドリル 小学生



場合の数 算数用語集




4年生向け 中学受験 算数 場合の数 組み合わせ計算 黒のボール2個と白のボール4個の並べ方をコンビネーションを使って求める方法を例題とともに解説します Youtube




場合の数 順列は2時間で解けるようになる 外資系コンサルタントが主夫になったら



1




組み合わせncrはどう計算する 求め方から性質までを攻略
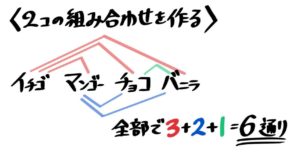



中学受験 場合の数の問題 解き方の総まとめ 数字カード 道順 色分け等 そうちゃ式 受験算数 新1号館 数論 特殊算




高校数学a Npr と Ncr の使い分け 練習編 映像授業のtry It トライイット
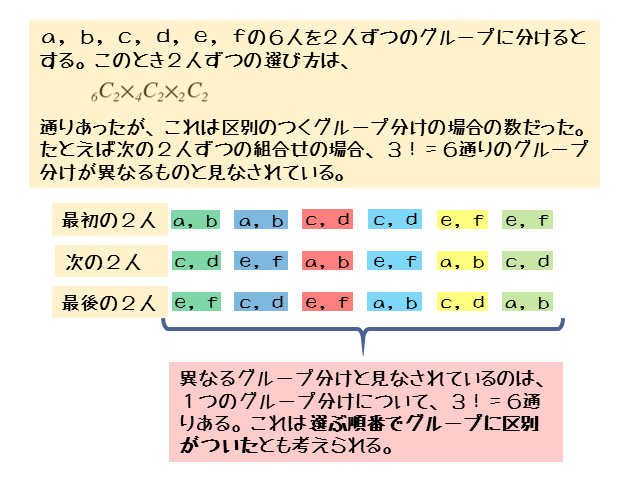



場合の数 グループ分けについて 日々是鍛錬 ひびこれたんれん




公式集 4 3 場合の数 組合せ 分ける 編 コメディカル受験対策講座



1



場合の数と確率を総まとめ 各種公式 重要記事一覧 受験辞典




高校数学a 組合せの活用2 男女の選び方 例題編 映像授業のtry It トライイット




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun



計算するから難しい 小学生の場合の数は 数え方 が大事 みけねこ小学校




場合の数と確率を総まとめ 各種公式 重要記事一覧 受験辞典




場合の数 順列は2時間で解けるようになる 外資系コンサルタントが主夫になったら




小学6年生の算数 場合の数 順列 練習問題プリント ちびむすドリル 小学生




高校数学 数a 17 組合せ 道順編 Youtube




算数 場合の数の解き方は 問題別に考え方を解説 数スタ




場合の数 組合せについて 日々是鍛錬 ひびこれたんれん




4年生向け 中学受験 算数 場合の数 組み合わせ計算 5人から 人を選びます コンビネーションを使った計算方法を例題とともに解説します Youtube
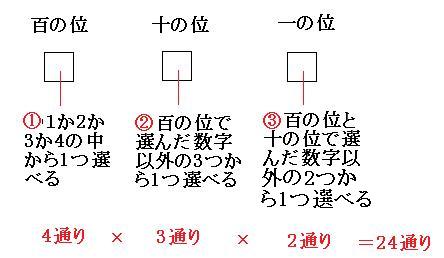



解き方解説 場合の数を計算で解く 場合の数は計算でサボれ




高校数学a 組合せの基本と順列との関係 Ncrの性質 受験の月




小学6年生の算数 場合の数 順列 練習問題プリント ちびむすドリル 小学生




場合の数 組合せについて 日々是鍛錬 ひびこれたんれん




組合せと順列は何が違うのか 組合せは樹形図でも計算でも解ける 計算 図 算数




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b
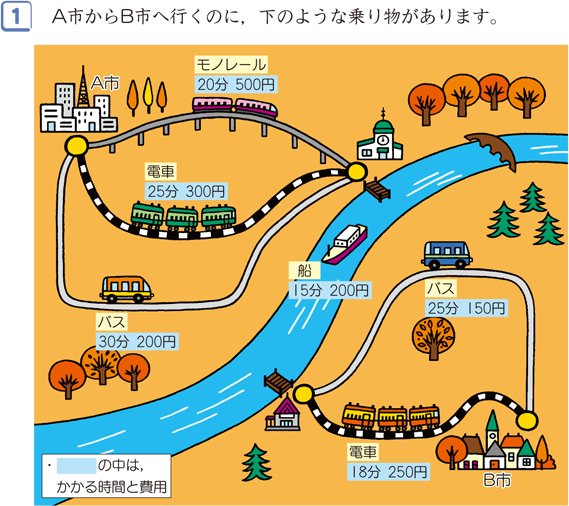



場合の数 算数用語集




場合の数 並べる と 選ぶ の計算方法の違い



場合の数 学び家 Com




順列の問題 一定の条件で並べる 高校数学の知識庫




高校数a 場合の数 Cの計算方法 オンライン無料塾 ターンナップ Youtube




高校 数学a 場合の数24 組合せの計算 15分 Youtube




場合の数 無料で使える中学学習プリント




山と数学 そして英語 場合の数と確率 組合せの公式と活用




小学6年生の算数 場合の数 組み合わせ 練習問題プリント ちびむすドリル 小学生



場合の数 組み合わせの計算方法について 高校数学マスマスター 学校や塾では教えてくれない 元塾講師の思考回路の公開




数学a 場合の数 組み合わせの総数 Youtube



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b




重複を許す組み合わせ Hを使った公式 仕切りを使った考え方を解説 数スタ
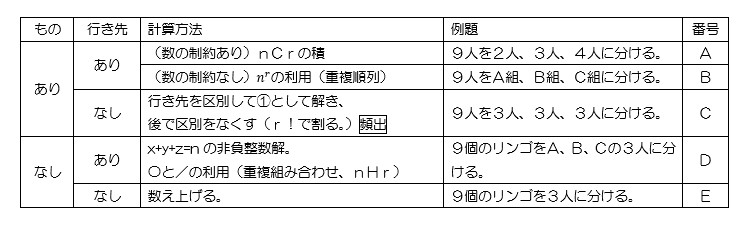



場合の数 確率を体系的に学ぼう 教科書でバラバラに登場するパターンを整理して把握しよう オンライン受講 東大に 完全 特化 東大合格 敬天塾




中学数学 場合の数




高校数学a 組分け問題全パターン 受験の月




順列と組み合わせの違いとは そしてそれぞれの意味を0から解説
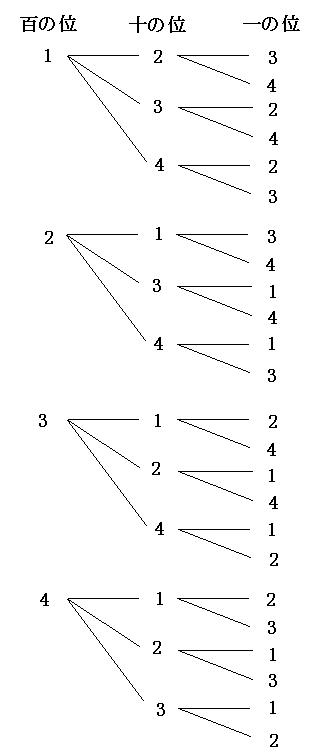



解き方解説 場合の数を計算で解く 場合の数は計算でサボれ




順列と組み合わせの公式とその違い 問題付き 理系ラボ



Q Tbn And9gcqk 07pns6gblxpztbesi Hjq Rmi0dl3bcobqphecjrlms6b O Usqp Cau




重複組合せはなぜ仕切りを使うの 整数解の個数を求める問題で鍛えよう 遊ぶ数学



1




場合の数 重複組合せ と 重複順列 の違いをわかりやすく解説します




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




場合の数 順列 P と組合せ C の違いは どう使い分ける ますますmathが好きになる 魔法の数学ノート
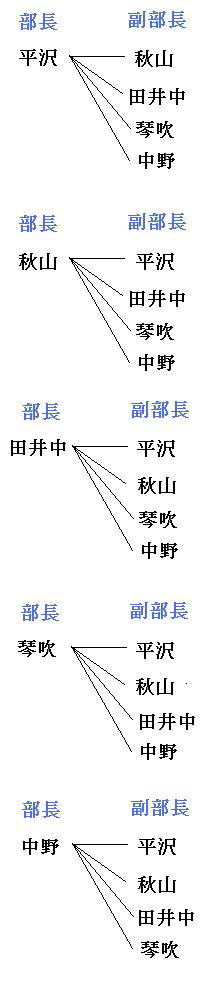



組合せと順列は何が違うのか 組合せは樹形図でも計算でも解ける




場合の数 組み合わせの計算方法について 高校数学マスマスター 学校や塾では教えてくれない 元塾講師の思考回路の公開




高校数学a 組合せの計算1 Ncr 練習編 映像授業のtry It トライイット




中学受験算数 これだけ 算数のカギ 場合の数 組み合わせの計算方法 Spi Youtube




場合の数 並べる と 選ぶ の計算方法の違い



うさぎでもわかる場合の数 順列と組み合わせの違い 工業大学生ももやまのうさぎ塾




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ



場合の数の一般問題 京極一樹の数学塾
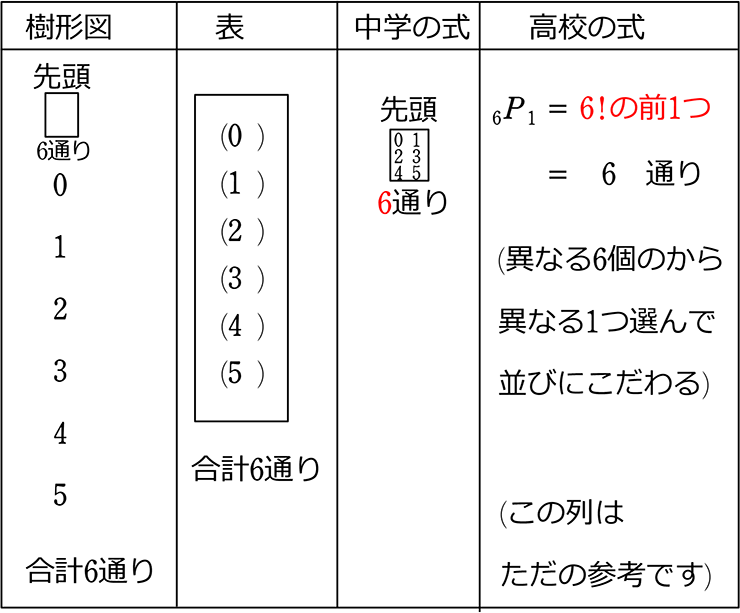



中学数学 場合の数




場合の数38 重複組合せの導入3 怜悧玲瓏 高校数学を天空から俯瞰する




高校数学a 組合せの活用4 少なくとも 映像授業のtry It トライイット




場合の数 同じものを含む順列について 日々是鍛錬 ひびこれたんれん
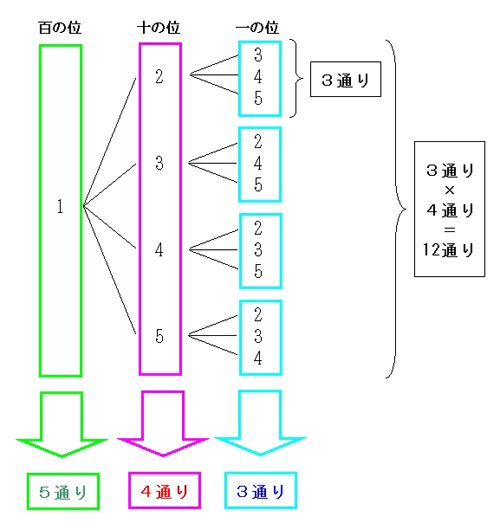



場合の数
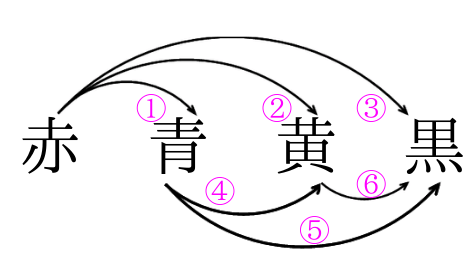



小学校で扱う場合の数の組み合わせの考え方 みけねこ小学校




中学受験 算数確認チェック29 場合の数 順列 組み合わせ グランパは元塾長




なぜ 同じものを含む順列の公式と使い方について問題解説 数スタ




重複順列と重複組合せ 感じる科学 味わう数学




数学a 場合の数 順列の問題か 組み合わせの問題かの見分け方 坪田塾 公式youtubeチャンネル Youtube




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ
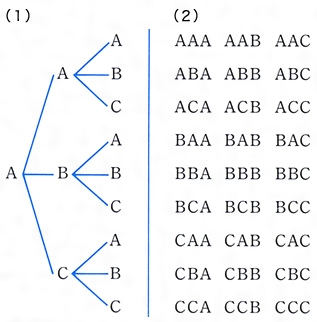



場合の数とは コトバンク



0 件のコメント:
コメントを投稿