小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題(2)円の面積、(4)球の体積について、 温故知新ラーニングのイメージ表現をしていきます。 (2)円の面積 (4)球の体積 2通りのイメージで求めてみます! 注)「偶関数」とは、縦のS(x)軸に関して対称の関V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積 ヘロンの公式 A = 面積 = bh/2 又は ヘロンの公式 jin
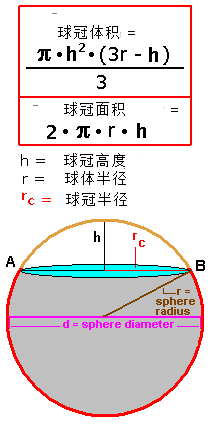
球冠在线计算器 在线计算 在线计算器 计算器在线计算
球 面積 体積
球 面積 体積-体積が分かれば表面積を計算できるケースがあるということを覚えておきましょう。 球の表面積の計算 それでは先ほど説明した立方体の表面積の計算方法で球の表面積を計算してみましょう。 まず球の体積\(V\)は\(\frac{4πR^3}{3}\)です。高次元の球とその体積とは n n n 次元(ユークリッド)空間において, x 1 2 x 2 2 ⋯ x n 2 ≤ R 2 x_1^2x_2^2\cdots x_n^2\leq R^2 x 1 2 x 2 2 ⋯ x n 2 ≤ R 2 を満たす点の集合を半径 R R R の n n n 次元球と言います。特に R = 1 R=1 R = 1 のとき,単位球と言います。




球面積計算球 Yxhsa
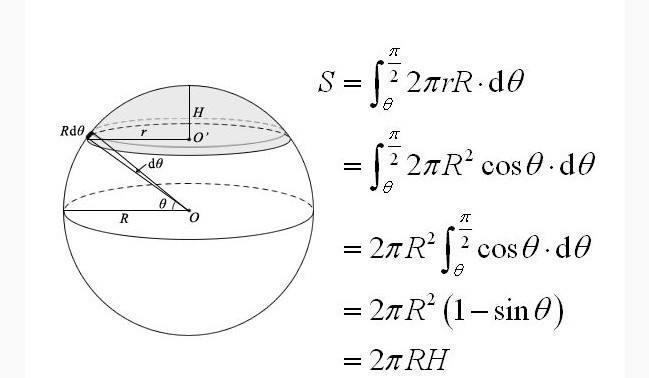
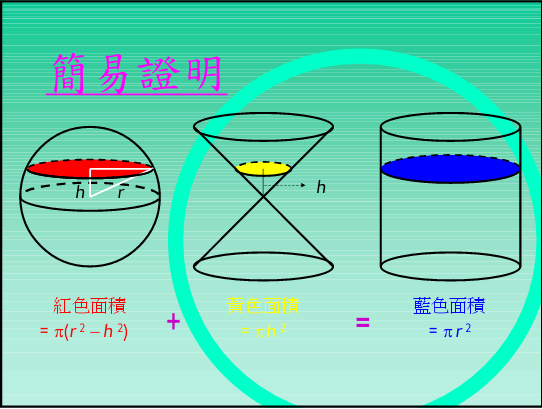
この状態で、2つの球の半径の差 $ \Delta r $ を限りなく 0 に近づけると、2つの球の表面積の差はほとんどなくなりますね。このとき、球殻の体積は、(半径 $ r $ の球の表面積 S)× $ \Delta r $ で求められるのです‼(← ここがポイント! 球の表面積 < (2) 2つの比較 (1)(2)より, < 球の表面積 < 方法②:輪切りにする 指針(考え方) この円柱の側面積= 球の表面積の公式と同じ式をしていることが分かる. あなたは今、球の表面積を求める公式を知らないものとします.体積」 により、理解されることだろう。 球の表面積 S と体積 V の関係式で、「3分の1」が乗ぜられるのは、この「3分の1」であ る。 カヴァリエリの原理を用いて、球の体積は、次のようにして求められ
球の体積基準比表面積(単位体積当たりの表面積) \(\displaystyle \frac {6}{D}\) 球の質量基準比表面積(単位質量当たりの表面積) \(\displaystyle \frac {6}{D \rho}\) 半分以上隠れている円の直径の推定 接触角の概算 円と球の空間球の表面積と体積 ここでは、球の表面積と体積を求める公式を紹介しましょう。 表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。 体積 続いて体積です。 球の半 まずは証明の前に,球の表面積と体積に関して認識しておくべきことを整理しておきました。 以下の語呂合わせで覚える方法が有名です: 球の表面積: 4 π r 2 4\pi r^2 4πr2 →「心配アール二乗」 球の体積: 4 3 π r 3 \dfrac {4} {3}\pi r^3 34 πr3 →「身の上に
球の体積 最後に、球の体積問題を解説します。 球の体積 \(V\) は $$ V= \frac{4}{3} \pi r^3 $$ という公式で求まります。 この公式がどうやって出てくるかを説明するには高校数学の積分が必要なんで、中学生はもう覚えてしまいましょう。 中学生でもおぼえられる「球の体積の求め方」 を解説していくよ。 球の体積の公式を忘れちゃったときに参考にしてみて。 球の体積の公式を1発で覚える方法 「球の体積の公式」を暗記する方法を伝授しよう。 3分の4 × 円周率 × 半径の三乗51 7 立体の体積と表面積 150 半径 3 cmの球と,その球がちょうど入る円柱,その円柱に ちょうど入る円錐がある。このとき,次の問いに答えよ。 ⑴ 球と円柱と円錐の体積の比を「球:円柱:円錐」と




球的面積公式球體的表面積公式 Pxmode



面积体积计算绿色版 面积体积计算软件下载v1 0 领航下载站
LNGタンク想定して、液面高さと表面積・体積の計算に使用 アンケートにご協力頂き有り難うございました。 送信を完了しました。 一部が欠けた球の体積 のアンケート記入欄 年齢 歳未満 歳代 30歳代 40歳代 50歳代 60歳以上 職業 小・中学生 高校5004nnn π=125π (cm2) (答) ※ 球の表面積は円の面積の4倍になる.(非常にきれいな関係) ※ 高校数学IIIで微分を習えば,体積 V= 43n πr3 を半径で微分すると表面積 S=4πr2 になることが分かる.脱線ついでに言えば,円の面積 S=πr2 を半径で微分すると 球を2つの平面で切り取ってできた球台について考えます。 Ⅰ 球台と球帯とは? Ⅱ 球台の体積 Ⅲ 球帯の面積 Ⅰ 球台と球帯とは? 前記事の「球欠と球冠」同様、聞き慣れない言葉である「球台」と「球帯」。まずはそれらの定義をお示しします。




球面積計算球 Yxhsa




球體的體積與表面積 人人焦點
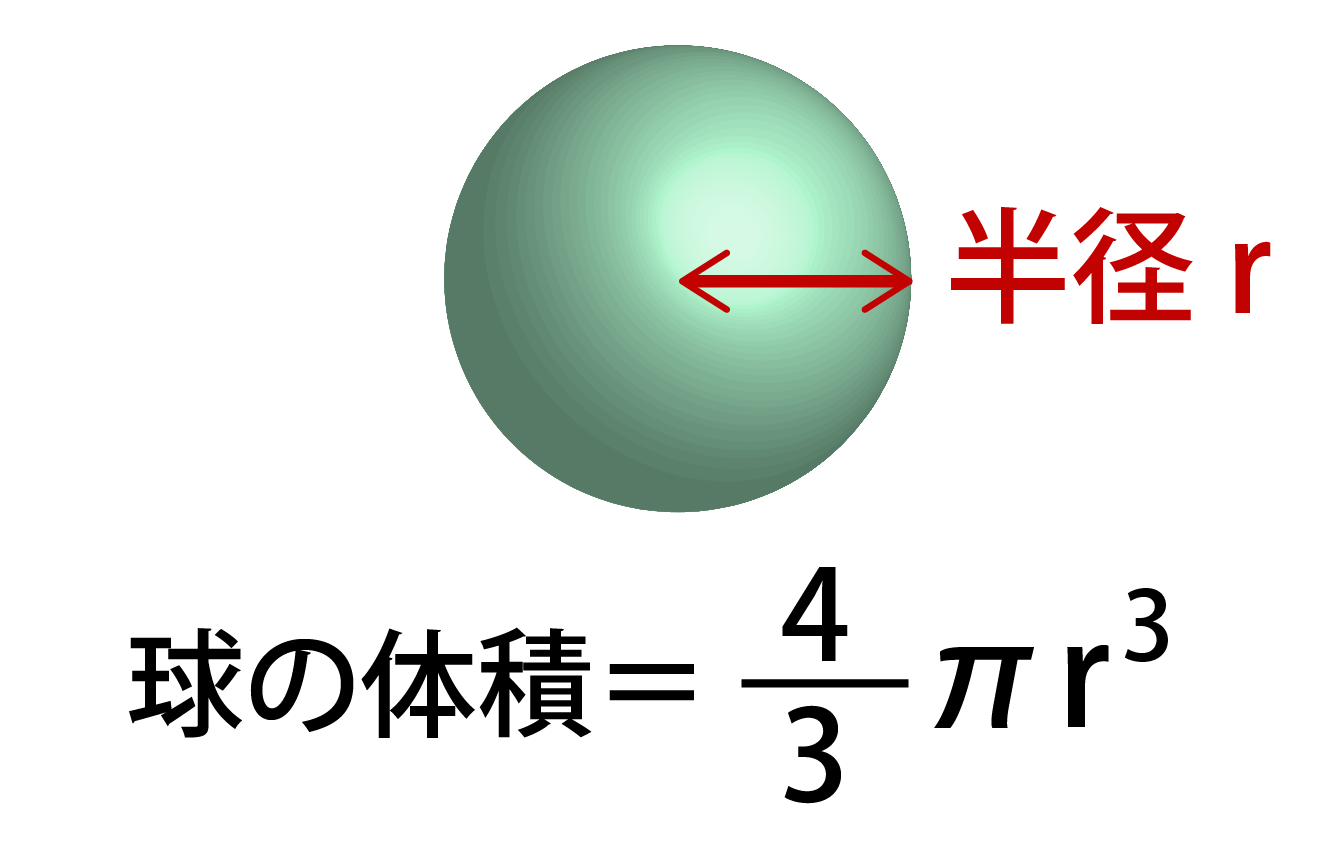
球 球の体積を求める公式は、次の通りです。 V = 4 3πr3 V = 4 3 π r 3 ここで、V は球の体積、r は球の半径、π は円周率を表します。 球の体積を求めるには、この公式に球の半径 r を代入すればよいだけです。 このページの続きでは、例題を使って、この球 ボール 体積計算 公式 求め方 計算方法 直径 半径 自動 円周率 volume楕円錐台の底面と上面の半軸と高さから体積、側面積、表面積を計算します。 球の体積 球の体積 球の半径から体積と表面積を計算します。 一部が欠けた球の体積 一部が欠けた球の体積 一部が欠けた球の体積と表面積を計算します。



多维球体的体积 小时百科



物理方法解决数学问题 二 Archimedes与球体积公式 Matrix67 The Aha Moments
の体積 V = 4 3πr3 V = 4 3 π r 3 体積 = 4 × 314 × 半径 × 半径 × 半径 ÷ 3 公式の 導出 ( どうしゅつ ) 方法と計算例は、「 球の体積の求め方 」をご覧ください。 球の体積の求め方一部が欠けた球の体積 非常に助かりました。 球を研磨したときの研磨体積を求めたかったのですが、入力するのがhでなくcの値を入力したかったです・・ 球を研磨したときの研磨体積を求めたかったのですが、入力するのがhでなくcの値を入力したかった 球欠,球台の体積と球冠,球帯の表面積 レベル ★ マニアック 積分 更新日時 球を平面で切り取った立体の体積,および側面の面積の求め方を解説します。 結果を覚える必要はありませんが,導出方法はマスターしておきましょう。 目次 球を




球帽球体积球楔比表面积 点公式png图片素材免费下载 图片编号 Png素材网




數學真魅 球體體積公式derivation Of Formula Of Volume Of Sphere
円の面積は A = πr2 A = π r 2 円周は ℓ = 2πr ℓ = 2 π r 球の体積は V = 4 3 πr3 V = 4 3 π r 3 球の表面積は S = 4πr2 S = 4 π r 2 この式を見比べていて、中学生の時の僕は何か規則性があることに気づきました。 円の面積 A = πr2 A = π r 2 の式において、 r2 r 2 の 2 2 を 球台と球帯 球を2つの平面で切り取ってできた球台について考えます。 Ⅰ 球台と球帯とは? Ⅱ 球台の体積 Ⅲ 球帯の面積 Ⅰ 球台と球帯とは? 前記事の「球欠と球冠」同様 n次元球の定義 n 次元球というのは n 次元の球です。 ちゃんと言うと、 n 次元空間内の「ある点」からの (ユークリッド)距離が「ある値」以下の空間を n 次元球と呼びます。 「ある点」を球の中心、「ある値」を球の半径と呼びます。 なお、今回は球の




如何计算球的体积 5 步骤




球的表面积与体积 怎么用微积分证明球的表面积和体积公式 三人行教育网 Www 3rxing Org
円柱の体積、表面積の求め方はこれでバッチリ! 円錐の表面積、中心角の求め方を解説!裏ワザ公式も! 円錐を転がすと1周するのにどれくらい回転する? 球の体積・表面積の公式はこれでバッチリ!語呂合わせで覚えちゃおう!←今回の記事




外接球体积的常见套路 几何 知乎




球面積積分球的體積 Itha




球冠 球缺的体积 面积 弧长 弦长在线计算器 三贝计算网 23bei Com
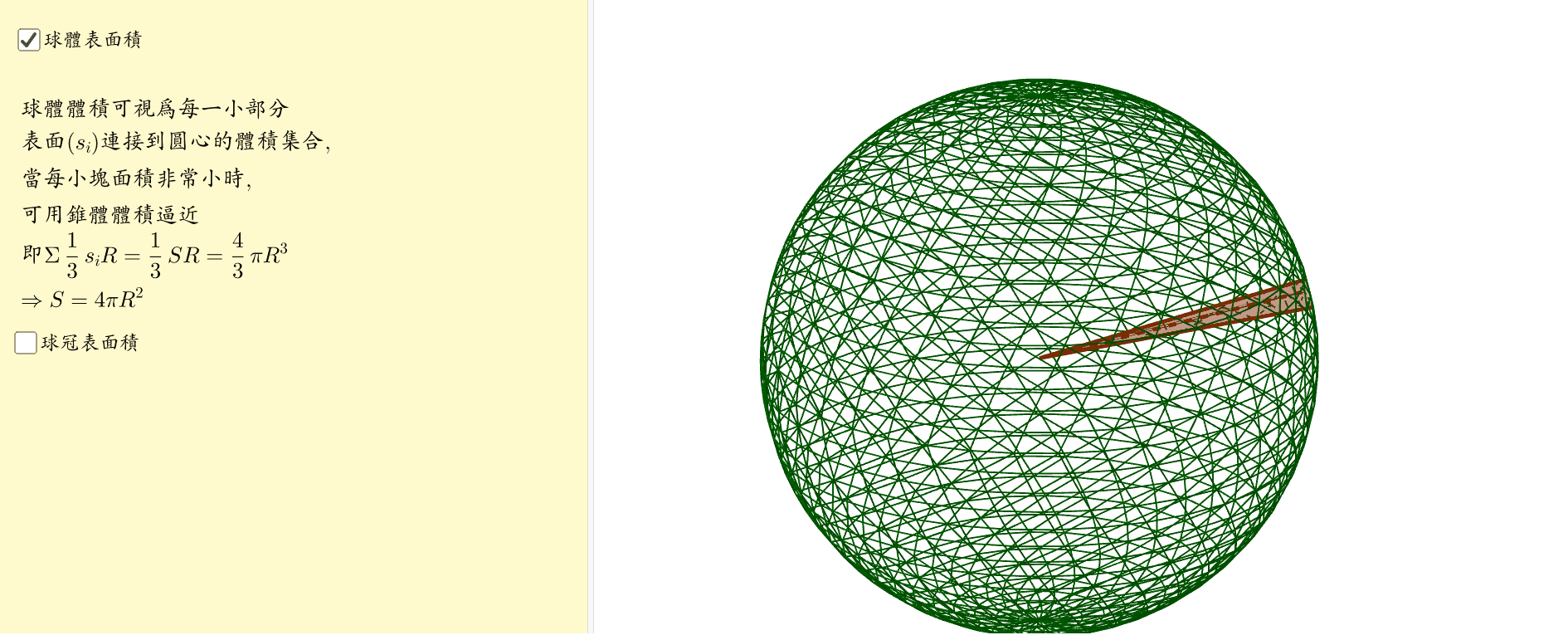



球體表面積 Geogebra




6park Com 祖冲之不止算出了圆周率 2 球体积和大明历




球體表面積球體 表面積 體積 Vhjk




球體表面積球體 表面積 體積 Vhjk




圆锥与球与圆柱




球的體積求導便是球的表面積 互為逆運算 降維與升維 每日頭條




圆球表面积公式用微积分如何推导 知乎



面积体积计算软件 面积体积计算软件下载v1 0 免费版 安下载



球的面积公式和球的体积公式是多少 扒拉扒拉




球面積體積用個橙話你知球體的表面面積 Ropux



球冠面积 球缺体积 简书




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



球冠 搜狗百科



高中数学必修2教案 1 3 2 球的体积和表面积 淘文库
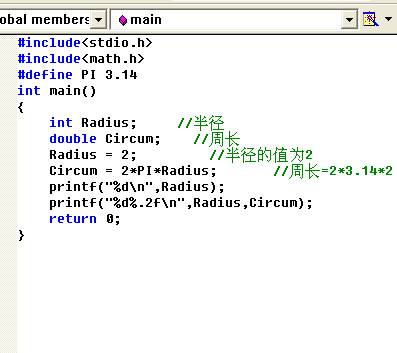



C语言输入半径求圆面积和体积 用c语言编写 输入半径r 求圆的周长 面积和球的体积 土亢不坑的博客 程序员资料



高中数学必修2教案 1 3 2 球的体积和表面积 淘文库




球的面積公式球體的表面積公式 Pxmode



3



在球的体积公式中 为什么会出现三分之四这个奇怪的系数 体积 公式 系数 新浪新闻



球的表面积公式和体积公式是什么 搜狗指南




科學月刊 大小有什麼差別 上




球表面積公式球體表面積 百度百科 Kmbymh




球面積計算球 Yxhsa




球面積計算球 Yxhsa
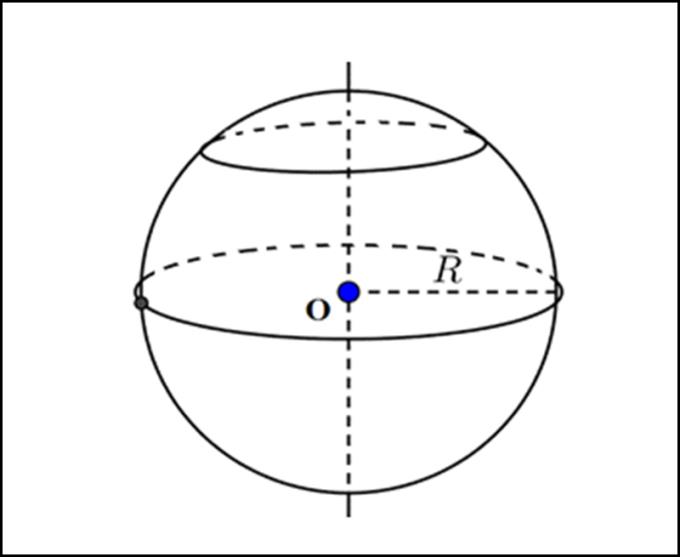



計算球體面積的公式 球體面積是完整而準確的




球體表面積體積球體表面積 球體表面積是指球面所圍成的幾何體的面積 它包括 Fefvw



球体体积公式 怎样计算球体的体积




012 球的体积空间几何体高中数学 Youtube




球的表面积例题 球的表面积和体积公式是什么 三人行教育网 Www 3rxing Org




球扇形 球心角体 体积 表面积计算公式与在线计算器 三贝计算网 23bei Com




球的表面积与体积 怎么用微积分证明球的表面积和体积公式 三人行教育网 Www 3rxing Org




積分球公式球的體積 Jvvx




球體面積積分為什麼球體積公式對半徑求導是球面積公式 而圓面積公式對半徑 Nkqun




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




積分球計算分光測色儀鞝理介紹 Fpgab




球冠 球缺的体积 面积 弧长 弦长在线计算器 三贝计算网 23bei Com




如何计算球的体积 5 步骤




球面積計算球 Yxhsa



球的体积求导便是球的表面积 互为逆运算 降维与升维 五四公社




球 圆球 体体积 表面积 周长 质量在线计算器 三贝计算网 23bei Com



球的表面積的求法 中學數學課 隨意窩xuite日誌




球冠体积公式 球冠体积公式



橢球 維基百科 自由的百科全書




球體表面積及體積的推導 每日頭條



1



球體的體積及表面面積 哔哩哔哩 つロ干杯 Bilibili



球体表面积推导图解第1页 驾考预约大全



球體體積 總表面面積 Youtube



球体体积公式推导图解 万图壁纸网




如何找到球的面积和体积 数学21



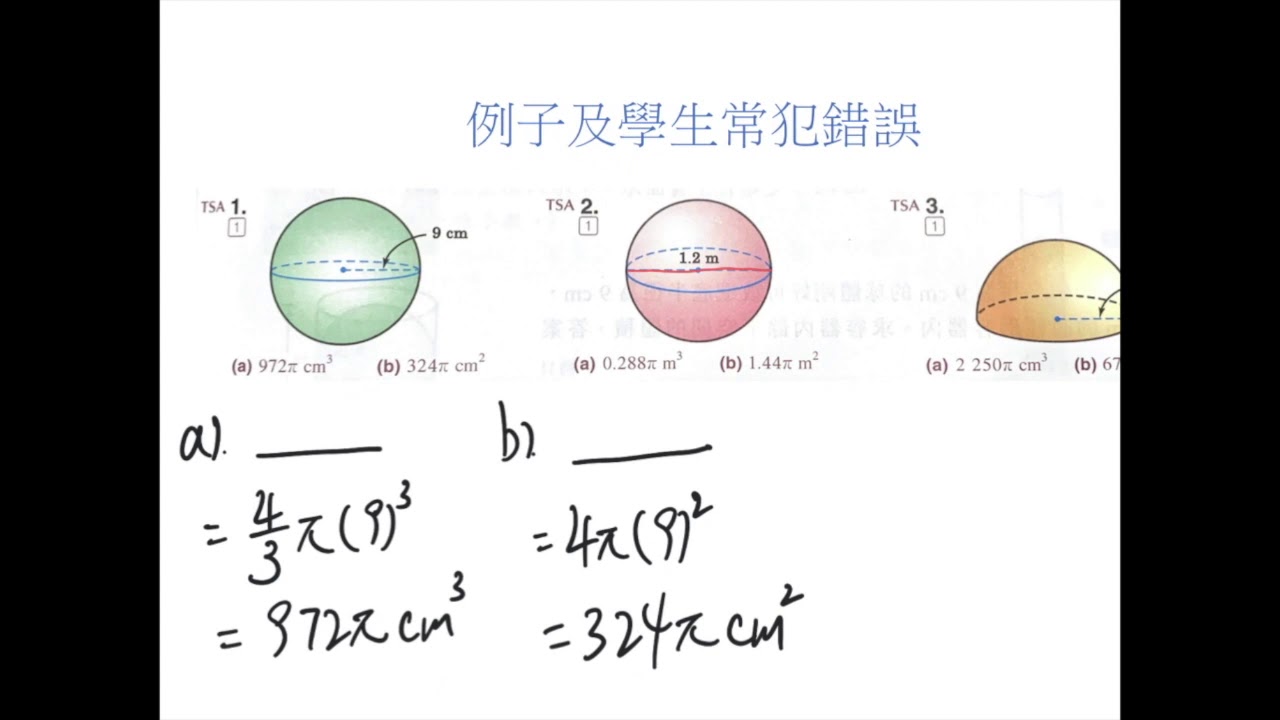
球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



球的體積




球冠在线计算器 在线计算 在线计算器 计算器在线计算




面積公式微積14 4 Lhlv




コンプリート 球体体積公式 犬イラスト




球体积计算公式




球の体積と表面積 Youtube



球體表面積球體 表面積 體積 Vhjk



柱 锥 台 球的体积公式推导 不用积分 Li Hua 博客园




球の表面積と体積の公式 数学fun




球體體積 Athlet




用感覺理解球體表面積公式 Youtube




面积体积计算软件 面积体积计算软件下载v1 0免费版 Pc6下载




球冠体积公式 球冠体积公式




球體表面面積用個橙話你知球體的表面面積 Nqnpg



圆球表面积 球体表面积的公式证明 篆体字转换器




椭圆体 椭球体体积 表面积计算公式与在线计算器 三贝计算网 23bei Com




球の表面積と体積の公式 数学fun




球面積積分球的體積 Itha



球体积的前世今生 新华网
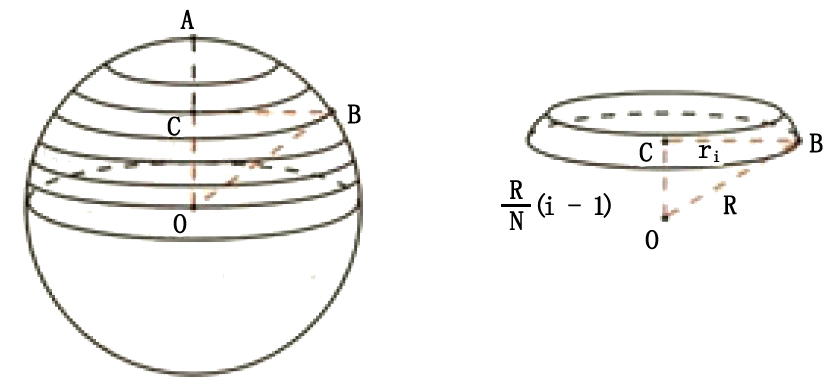



球的体积公式推导 孤云出岫 去留一无所系 朗镜悬空 静躁两不相干 Csdn博客 球的体积公式推导过程




球體表面積 球體表面積是指球面所圍成的幾何體的面積 它包括球面和球面所圍 華人百科



圆球表面积 球体表面积的公式证明 篆体字转换器



1



球冠体积计算公式附图 第1页 要无忧健康图库



球的体积求导便是球的表面积 互为逆运算 降维与升维 五四公社




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学




Relationship Between Volume And Surface Area Of A Sphere 球體的體積與表面面積的關係 Geogebra




體積計算公式體積公式 百度百科 Mrsysy



円柱とそれに内接する球の表面積比と体積比について 久保塾 今治市の学習塾




球の体積と表面積の公式をごちゃまぜにしない2つのポイント Qikeru 学びを楽しくわかりやすく




球缺體積和球冠表面積的計算公式及應用 It閱讀




球的体积公式推导图文 如何用微积分知识推导球的体积公式 三人行教育网 Www 3rxing Org




球台球带体积 侧面积 表面积计算公式与在线计算器 三贝计算网 23bei Com




圆球体积公式 球形面积计算公式图解 环球信息网
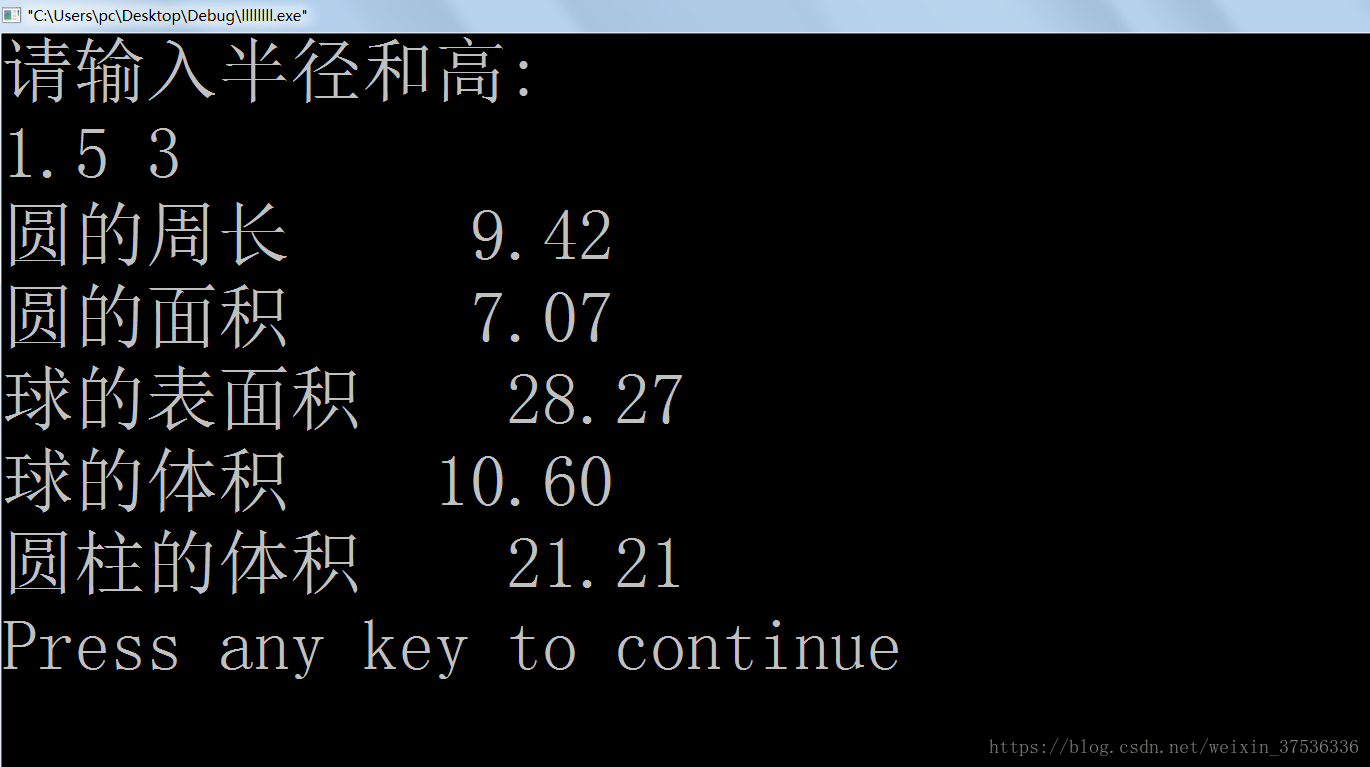



圆半径r 1 5 圆柱高h 3 求圆周长 圆面积 圆球表面积 圆球体积 圆柱体积 希望能对学习c语言的朋友有帮助 程序员信息网




胶囊罐体 球冠高等于柱体半径 体积 表面积计算公式 三贝计算网 23bei Com




球表面積計算球的體積 Jlxpis
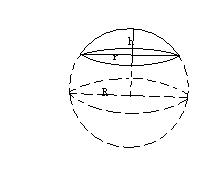



球缺 維基百科 自由的百科全書



在球的体积公式中 为什么会出现三分之四这个奇怪的系数 体积 公式 系数 新浪新闻



1



0 件のコメント:
コメントを投稿