3 北海道⼤学Hokkaido University 情報理論講義資料 巡回符号の定義 n符号多項式:符号語の多項式表現 0, 1 からなる長さnの符号語v=(v n-1, v n-2,・・・, v 1, v 0) を V(x) =v n-1 xn-1+v n-2 xn-2+・・・v 1 x+v 0 で表す。 ⇒符号長nの符号は、n-1次以下の多項式の集合とし 2 つの 32 ビットまたは 64 ビットの符号付き整数の商を返し、出力パラメーターの剰余を返します。 Exp e (自然対数の底) を指定した回数だけべき乗して返します。 Floor 指定した Decimal または Double の数値以下の最大の整数を返します。 IEEERemainder22 生成多項式とは 符号長が n の符号語を (a 0, a 1, a 2, , a n1 ) としたとき、これを変数 x の多項式 F(x)として 次のように表します。 (n1)次以下の多項式は全体で2 n 個存在しますが、その中でk次の特別な多項式 G(x) で 割り切れるものだけを符号として扱うことを考えます。

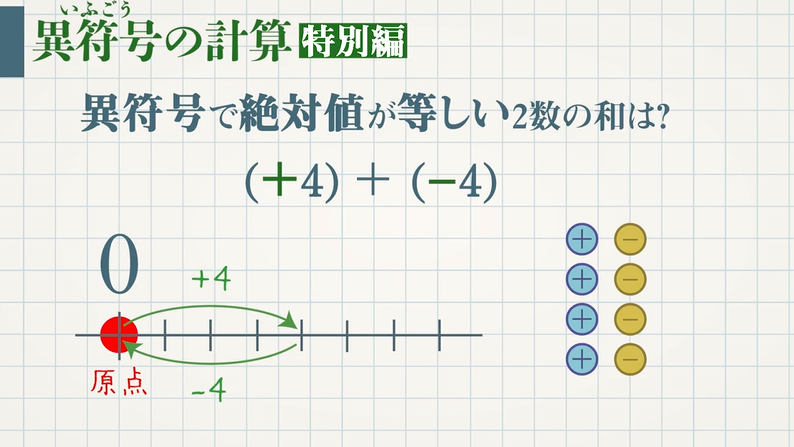
中学数学1年 正負の数の加法と減法 加減の混じった計算 受験の月
符号の計算 問題
符号の計算 問題- ここで,符号の長さは n ビットとする。 〔 n ビットの符号を求める計算手順〕 (1) 左端及び右端のビットが 1 である ( n 1) ビットのビットパターン (以下,マスクという) を定める。 (2) 符号計算対象のビット列の右端に n ビットの 0 を付加したビット列を情報符号理論 17 4 平均符号長の限界と情報源符号化定理 西田豊明 5 / 6 𝑛が増加するにともない,平均符号長が𝐻1(𝑆)≈0469に漸近している様子がわかる. 44 情報源符号化定理



途中このような計算式になった場合 この符号はいわゆる同符号 異符号 また そ Yahoo 知恵袋
最上位ビット (msb) は負の数を表しますから、 8 ビットの符号つき 2 進数では、 これが "1" の場合 1 × 2 7 = 128 になります 。 したがって上表の通り、 8 ビットの符号つき 2 進数、"" は 128 で、 "" は 127、 "" は 1 です。2 と 7 はともに符号が「」で同符号である。この2数の絶対値の和(27)に共通の符号「」をつければ答えとなる 確認 答表示 次の計算をせよ。 (10) (6) 16 (15)(6)21 (12)(05)17 練習 同符号の和 ≫ 異符号の和 絶対値の 差 に、 絶対値の大きい方の受信符号語の誤りを見つける方法 u =(x 1, x 2, x 3, x 4, c 1, c 2, c 3 ) 長さ7のハミング符号語 ただし、 c 1 =x 1 +x 2 +x 3 c 2 =x 1 +x 3 +x 4 (mod 2) c 3 =x 2 +x 3 +x 4 新たに、次の3つの量を計算する。 s 1 =x 1 +x 2 +x 3 +c 1 s 2 =x 1 +x 3 +x 4 +c 2 (mod 2) s 3 =x 2 +x 3 +x 4 +c 3 よって、u
★ご注意ください★ この計算をあいまいにしてしまって『数学が苦手』になる生徒も少なくないのでご注意ください。 計算はトレーニングしだいだから頑張って! 正負の数の加法 加法と減法とは『加61符号化復号化システム また,符号化比率(code rate, rate) r は r = (log2 M)/n = k/n, (124) で与えられる†. ,長さn の2元ベクトル (2n 個) (n,k,d) 符号の符号語(M =2k 個)d v1 v2 v M v3 Bn = {0,1}n 図121 符号化の概念 例121 図12 の偶数(または奇数)パリティ検査符号(even parity check code)は(9,8,2) 符号である.符号長 𝑛𝑛 の符号は,𝑛𝑛−1次以下の多項式の集合として表せる このとき,各符号語に対応する多項式を符号多項式と呼ぶ 5 例87) 𝒗𝒗= (1,0,1,1,0) 𝐹𝐹𝑥𝑥= 𝑥𝑥 4 𝑥𝑥 2 𝑥𝑥 変数 𝑥𝑥に大きな意味はない 単に係数を区別するための
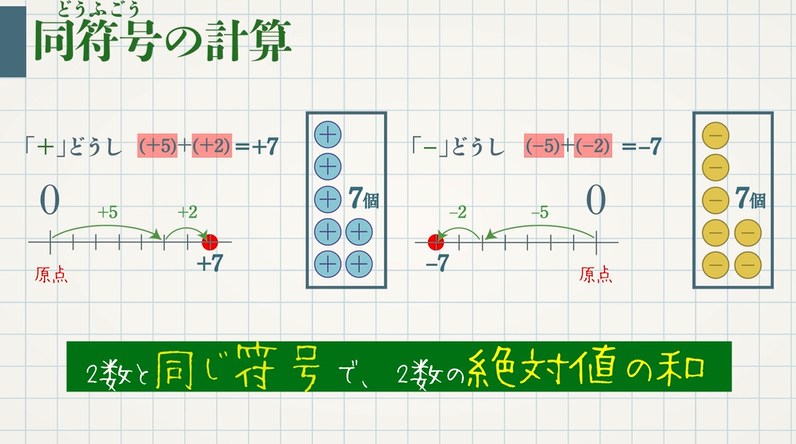
コンパクト符号の符号木 における最高次の葉 𝑁𝑁 ※ 証明は教科書を参照のこと コンパクトな瞬時符号の符号木において,最も長い 符号語に対応する葉は少なくとも二つあり,それらの どの葉に対しても共通の親を持つもう一つの葉が存 在する.に属する通信路符号であり,次の顕著な特徴を有している. 符号長nに対して符号化と復号がO(nlogn) の計算複雑 度で実装可能であり,この復号は逐次除去復号と呼ばれる. 符号化レート(伝送速度) が対称通信路容量よりも小さ ければ,任意に固定した0同符号の2数の加法(足し算) 同符号の2数の和は、絶対値の和に共通の符号をつけたものです。 (+3)+(+2)=+(3+2)=+5 (-3)+(-2)=-(3+2)=-5 練習問題 次の計算を




中1 中学数学 解答 同符号の正の数 負の数の計算 練習問題 中学生 Clear




足し算 加法 正負の数 中学1年 数学の楽園
ふつうの計算問題(3つの数字) ふつうの計算問題(2つの数字) 虫食い算 符号入れ 漢数字の計算ドリル 問題数 10問 問 30問 40問 50問 New 100問 解答 印刷する 印刷しないバイト換算 異なる単位の容量計算の際に使用しています。 Windows10のパーティションのバイト換算に使わせていただきました。 便利です! GCPの見積もり取得でデータ量把握のため使用させていただきました。 データ使用量を調べるのにつかいました誤り訂正符号の基礎 • 7,4,3ハミング符号について インターネット工学 誤り訂正符号 送りたいビット 計算したビット 情報ビット パリティ検査ビット 受信側で 整合性を調べる p59~60 2 インターネット工学 フレームの誤り訂正




世界一わかりやすい数学問題集中1 1章 正の数 負の数




正負の加減の計算を覚えよう 数学嫌いな子のための簡単理解法 分かりにくいを分かりやすいに
1番単純な通信路符号としてパリティ検査について考える。パ リティ検査は1誤り検出符号になっている。 パリティ検査符号は以下の形式になる。 w = ()xx x p 11 12 1N 1 ( ,, , ,n) n − − " ビット 1ビット 情報ビット 冗長ピット これらに関係する概念を順にみてのとき、「符号を取り除いた2つの数」は 7 と 4 です。 そこで、「大きい方から小さい方を引く」と 7−4=3 になります。 大きい方の符号+付けて、 −3 (答) 以上の計算は、次の形にまとめることがこれらの計算結果から,一般に引き算も2進数の和で計算できることが分る。 つまり加減共に同一の回路で計算できることになり, 回路が単純化でき処理が速くなる という利点が生まれる。そのため,2の補数を負の表現として採用しているシステムが多い
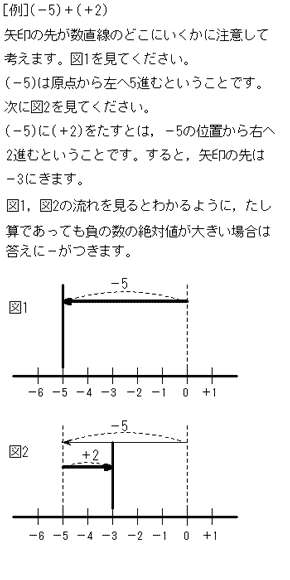



正負の数 異符号の加法の符号はなぜ絶対値大のほう 中学生からの勉強質問 数学 進研ゼミ中学講座
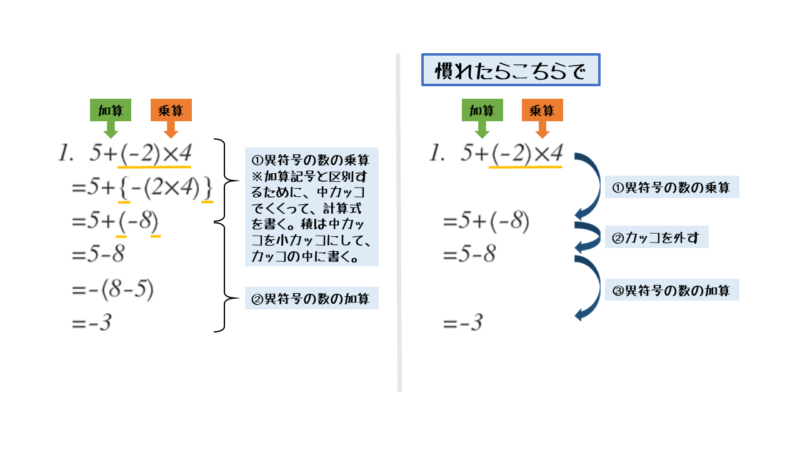



中学数学 正負の数の四則混合算を解いてみよう 日々是鍛錬 ひびこれたんれん
が返されます。 使用例 b2セルには=dec2bin(a2) e2セルには=dec2bin(d2) と入力されています。 2進数を10進数に変換します。 topへ バイナリ・トゥ・デシマル2進数の最上位のビットは符号を表します。 数値 < 512 または数値 > 511 の場合、エラー値 #num!対応のある2群のノンパラメトリック検定:表計算ソフトで行うWilcoxonの検定 Wilcoxonの検定は対応ある2群のノンパラメトリック検定 の一つです。 次のようなデータの検定に利用します。 ・アンケートやVASで計測したデータの順位は正しいという仮定を利用




今日から使える 計算ミスを減らしてテストの点数を上げる方法を紹介 成績プラス




数学の計算でミスする原因はこれ 都立に入る
32 符号間干渉とアイパターン 符号伝送速度が与えられたとき,伝 送帯域幅を最小 図2 tdma方 式の原理 図3 2値符号雑音の振幅確率分布から符号誤り率 の計算 図4 2値符号の信号対雑音比と符号誤り率の関係 講 座 ディジタルテレビジョンの基礎 (69)3また、符号の数が少ない方の個数をrとする。 帰無仮説が成立するならrが出現する確率は であり、二項分布に従うことになる。この計算によってr値がその値以上の極端な値をとる確率を求める。 データの数nが5<n≦25ならば直接計算して確率を求めればよい。正の数・負の数の加法は,次のように計算すればよい。 ・同符号の 2 数の和 2 数の絶対値の和に共通の符号をつける。 ・異符号の 2 数の和 2 数の絶対値の大きい方から小さい方をひき,絶対値の大 きい方の数の符号をつける。
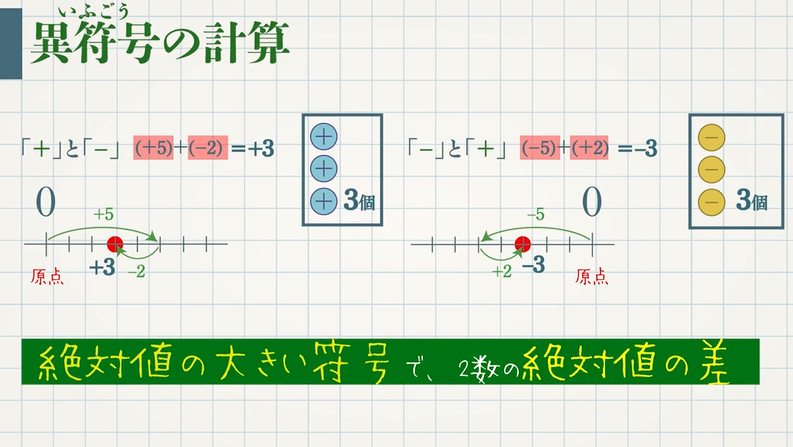



正負の数の加法 足し算 教遊者




中学数学 正負の数の加減算を解いてみよう 日々是鍛錬 ひびこれたんれん
一意復号可能な符号の構成可能性 マクミランの不等式 l 1, l 2, , l M q− 1 q− 2 q − l M ≤1 長さ の M個の符号語 1 2 ,c M をもつ元一意復号可能な符号q を構成できる. ⇔ 瞬時符号 一意復号可能符号 クラフトの不等式を満たす 符号長をもつ符号を講義目次 •8相互情報量と通信路容量 •813 通信路容量 •814 通信路容量の意味 •815 通信路容量Cの計算例 •816 今までの整理:情報源と通信路 •817 シャノンの第1定理 •9 雑音通信路での高信頼情報伝送 •91 雑音のある通信路 •92 雑音のある通信路での符号化 この符号の付け方は 2 10 = 1024 通りありますが,順位和が 52 以上になるのは全部 にした場合と二つの 15 のどちらかに − を付けた場合の3通りです。



Http Www Shinjuku Ed Jp Jh Ushigome1 45 Pdf




異符号どうしの足し算 Youtube
となる。 mod 2 の計算での に気をつけて、実際に計算をすると、 符号多項式ですべての符号多項式を割り切り(の因数となり)、最小次数のものをその巡回符号の生成多項式という。 定理(構成法1) U を長さnの巡回符号とする。 u(x)=p(x)g(x) ( g(x):Uの




数学 For 大学受験 おそらくこの計算方法を植え付けるためだけに 絶対値 という用語をこの直前に取り上げているように思える この方法だと 同符号の場合 と 異符号の場合 で 違う手続きを暗記しないといけなくなるという点でよろしくない



Www City Hamamatsu Szo Ed Jp Kaisei J 5 1 homework 2 Suugaku Suugaku1 Pdf



公立高校受験予定の中学3年生が未だに正負の数の加法 減法 乗法 除法の Yahoo 知恵袋



Http Tyu Oita Ed Jp Hita Toubu Ef 91 E5 B9 B4 E7 Ac Ac Ef 91 E7 Ab A0 80 8c E6 Ad A3 E8 B2 A0 81 Ae E6 95 B0 80 8d E5 8d 98 E5 85 81 Ae E6 8c 87 E5 B0 8e E8 A8 E7 94 Pdf




正負の乗除の計算を覚えよう 数学嫌いな子のための簡単理解法 分かりにくいを分かりやすいに
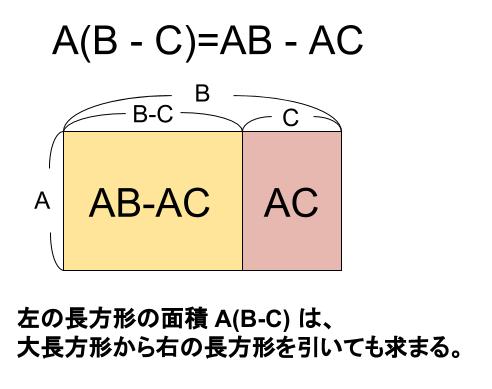



分配の法則 符号ミスがなくなる決定版 中学数学の無料オンライン学習サイトchu Su



この増減表のy の符号って計算せずに出す方法ってありますか 元の関数の次 Yahoo 知恵袋




正負の符号 こんな動画教材どうですか テーマで学ぶ中学校数学




中1の数学 正負の数や文字式 方程式は中学数学の基礎 家庭教師ジャニアス




正負の数の加減 生徒の発想を見習った 代数和計算法を基本に 計算順序を見直す提案 コロンブスの卵的発想で実に単純な話です Ppt Download




1 15 プラス マイナスの計算で言い残したこと 前 なぜ は符号と演算で一緒にしたのか 理一の数学事始め Note




Descubre Como Resolverlo En Qanda



正負の数の加法 足し算 教遊者




正負の数の減法 引き算 と 加法と減法の混じった計算 教遊者
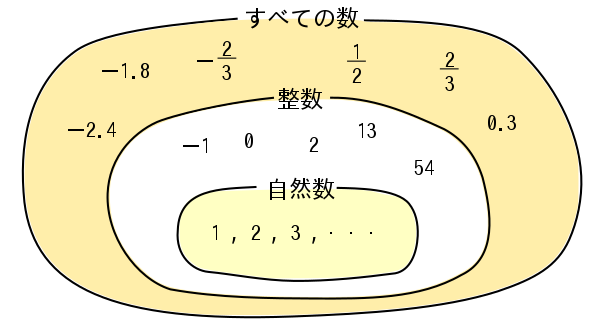



中学校数学 1年生 数量 正負の数 Wikibooks



1



正負の数の加法 足し算 教遊者




加算減算除算シンボルラインの乗算教育コンセプト数学は白い背景に符号を計算し基本的な数学記号プラスマイナス乗算アウトラインの除算ベクトル アイコンのベクターアート素材や画像を多数ご用意 Istock




加算減算除算シンボルラインと固体を乗算し教育概念数学は白い背景に符号を計算し基本的な数学記号プラスマイナス乗算とアウトラインで除算ベクトル アイコンのベクターアート素材や画像を多数ご用意 Istock




数学符号




小 中必見 単元別解説 四則演算 加減法編 学習内容解説ブログ




5 3p33sqrt3 Descubre Como Resolverlo En Qanda



計算ミスを無くすには 塾長の講義とつぶやき



カッコの外し方 カッコの前にマイナスがあると符号がかわる 三重の個人契約家庭教師




中学数学1年 正負の数の加法と減法 加減の混じった計算 受験の月



目指せ 建築士 濱崎塾 カリスマ講師の学習アドバイス 日建学院



Cms Oklab Ed Jp Jh Rokuhoku Index Cfm 1 1235 C Html 1235 0624 1616 Pdf




電卓 計算式の符号表示 By Shino Kai



h22 aki fe pm q03 qus 基本情報 応用情報 問題と解説




負の数の足し算 引き算 数学fun
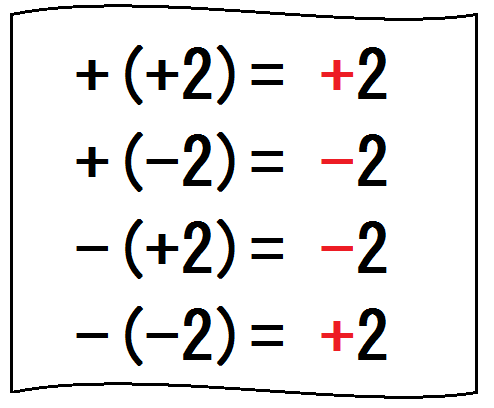



中学数学 正負の数 でつまずく原因と解決法 加減 かっこ外し



1 5第1章加法 正負の数の加法 同符号 中学生




学習指示 中1 数学 P23 加減混合計算 1 坂東市進学塾 スタディ ポート 港日記 楽天ブログ




5 Descubre Como Resolverlo En Qanda




中1 P 26 正負の数の計算特訓 Youtube




21 号 ターボ積符号の復号方法 装置 およびコンピュータ読み取り可能な記憶媒体 Astamuse




Crc Ouyou




正負の数 加法 減法のやり方はコツがある 中学数学 理科の学習まとめサイト




中学数学 正負の数 でつまずく原因と解決法 加減 かっこ外し
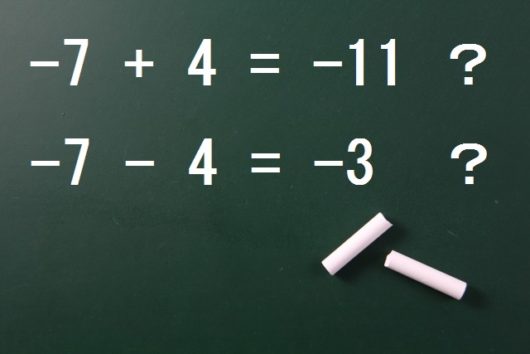



中学数学 正負の数 でつまずく原因と解決法 加減 かっこ外し



中2数学 基本解説プリント12 式の計算2 加法 減法 問題 2




正負の数 計算の仕方 コツ 加法 減法をマスターしよう 数スタ




加算減算除算シンボルの細い乗算教育の概念数学は白い背景に符号を計算し基本的な数学記号プラスマイナス乗算アウトラインの除算ベクトル アイコンのベクターアート素材や画像を多数ご用意 Istock
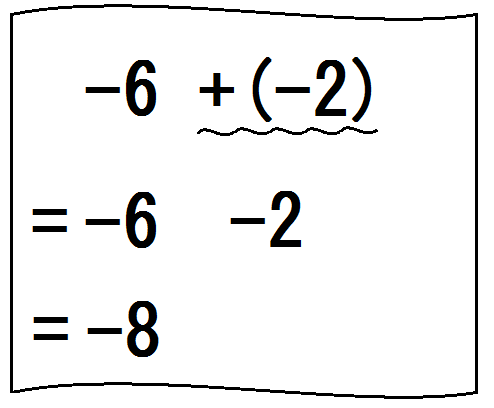



中学数学 正負の数 でつまずく原因と解決法 加減 かっこ外し



1




正負の数 計算の教え方 算数オンライン家庭教師 倉永 将太朗 Note




中学数学1年 1章 正の数 負の数 3 乗法と除法 9時間 Ppt Download



1




数学動画教材1105 01 テーマ 加法の素早い計算方法が理解できる について こんな動画教材どうですか テーマで学ぶ中学校数学




中学1年生 数学 無料問題集 正の数 負の数の減法 引き算 おかわりドリル
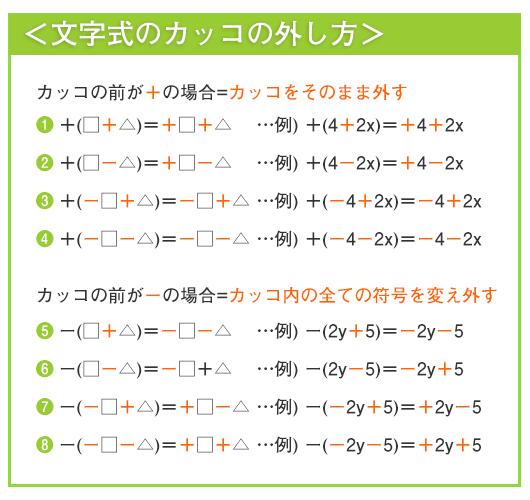



中学校1年生数学 文字式の計算 カッコの外し方 長野地区 Itto個別指導学院 長野市の学習塾




本時の目標 正の数 負の数の加法の計算のしかたについて理解し その計算ができるようにする Ppt Download



C言語のキャストについて解説 符号あり と 符号なし の比較 計算は特に危険 だえうホームページ




中1 数学 中1 4 正負のたし算 ひき算 Youtube




正負の数の除法 逆数 乗法と除法の混じった計算 教遊者



白い背景に数学のアイコンフラットスタイルあなたのウェブサイトのデザインロゴアプリuiのための数学と番号のアイコン数学的計算記号数学的計算は符号です アイコンのベクターアート素材や画像を多数ご用意 Istock




数学 新 中1編 正負の数 加法 足し算 小4から始める高校受験 お母さん 一緒にがんばりましょう




2進符号 計算 トンネル 抽象的 技術 提示 2進符号 計算 トンネル 抽象的 緑 技術 提示 Canstock




21 号 ターボ積符号の復号方法 装置 およびコンピュータ読み取り可能な記憶媒体 Astamuse
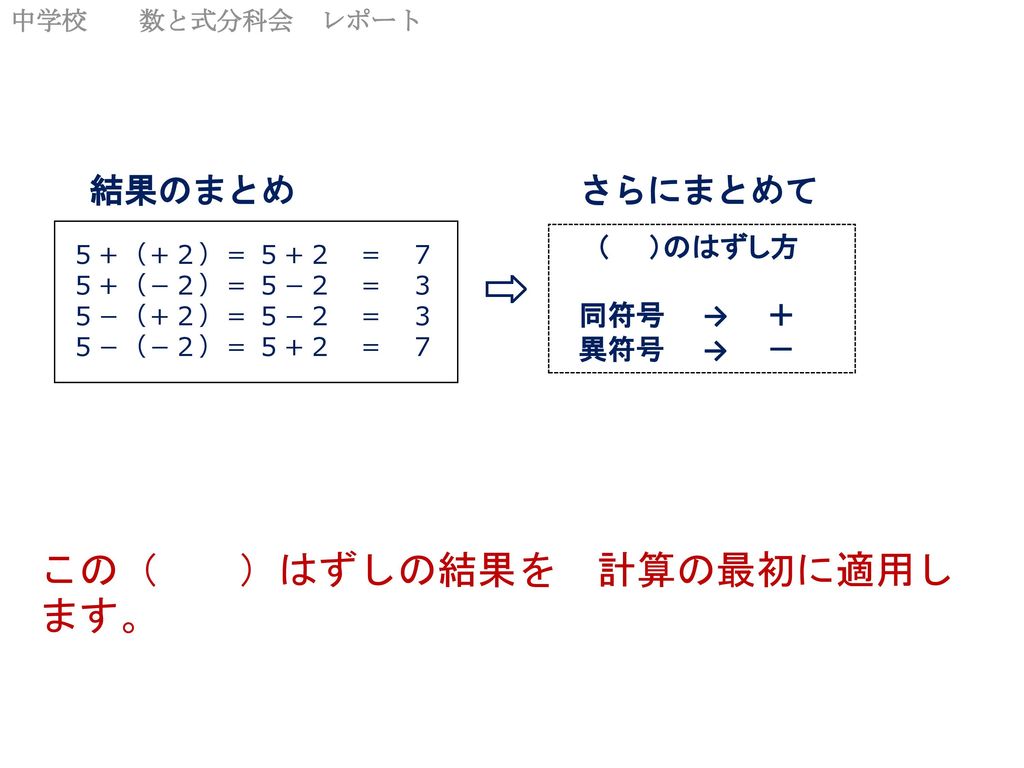



正負の数の加減 小学校算数に接続した 8時間教材が 4時間で完了する 単元構成の提案 教科書の書き変えを願って Ppt Download
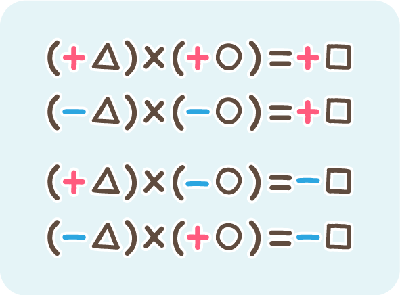



中1の数学 正負の数や文字式 方程式は中学数学の基礎 家庭教師ジャニアス
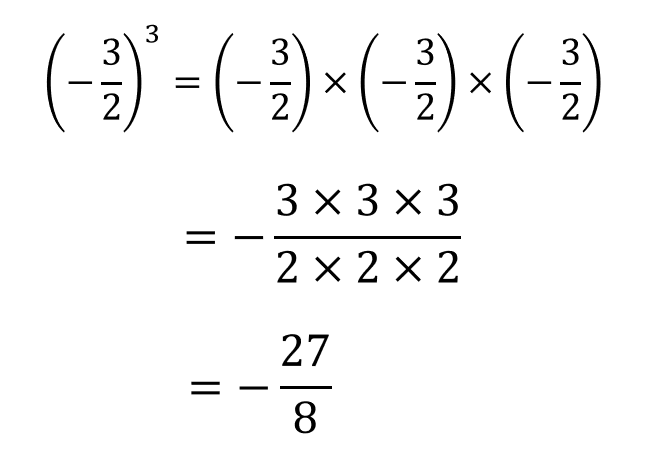



中1数学 正負の数 分数計算のやり方を問題解説 数スタ




小 中必見 単元別解説 四則演算 マイナスの考え方 学習内容解説ブログ



1




中学1年生 数学 正負の数 加法 減法 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



この計算ってどうして の符号になるんですか 理由を分かる方は教えてく Yahoo 知恵袋



なぜこの場合の計算では2pを移行すると符号がマイナスでなく分数になる Yahoo 知恵袋




小 中必見 単元別解説 四則演算 加減法編 学習内容解説ブログ




正負の数 加法 足し算 と減法 引き算 のやり方 中学数学 By Okボーイ マナペディア



途中このような計算式になった場合 この符号はいわゆる同符号 異符号 また そ Yahoo 知恵袋



Www Chuo Tky Ed Jp Ginza Jh Resources Content 9998 0507 Pdf
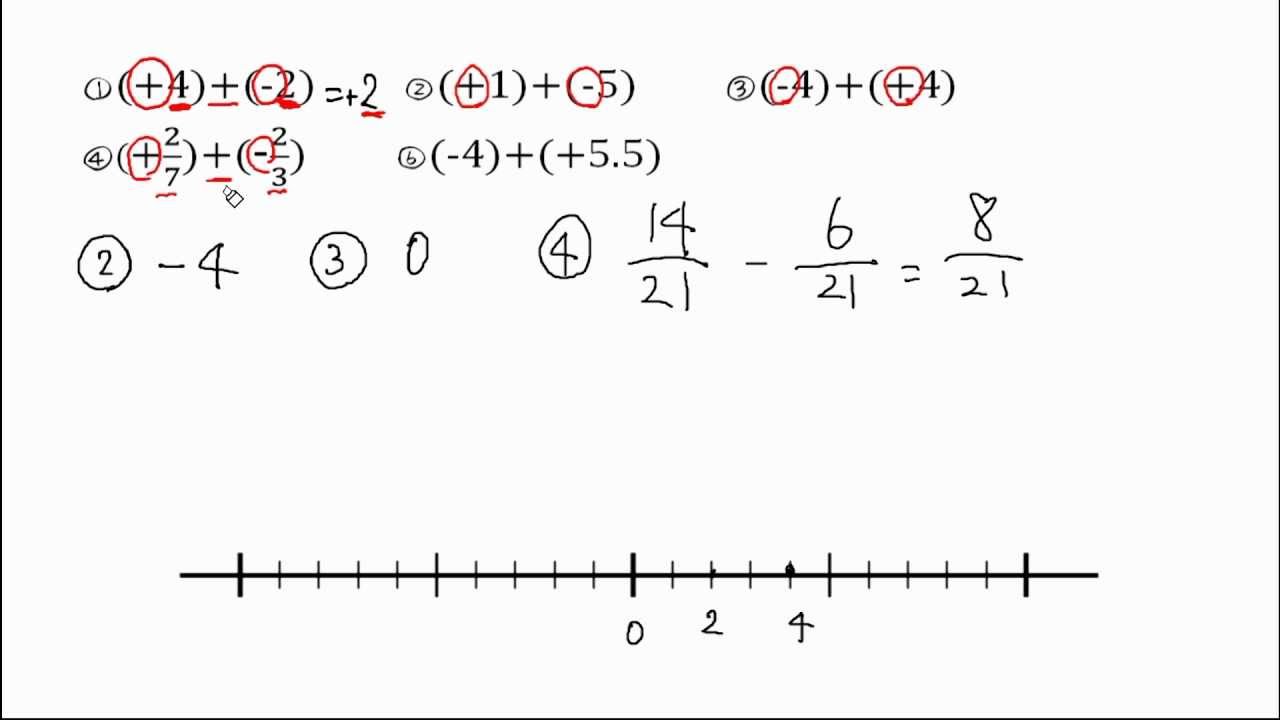



異符号どうしの足し算 問題 Youtube




そこそこ長い計算が必要な問題で 符号間違えだけだった問題ってもう一度解き直した方がい Clear
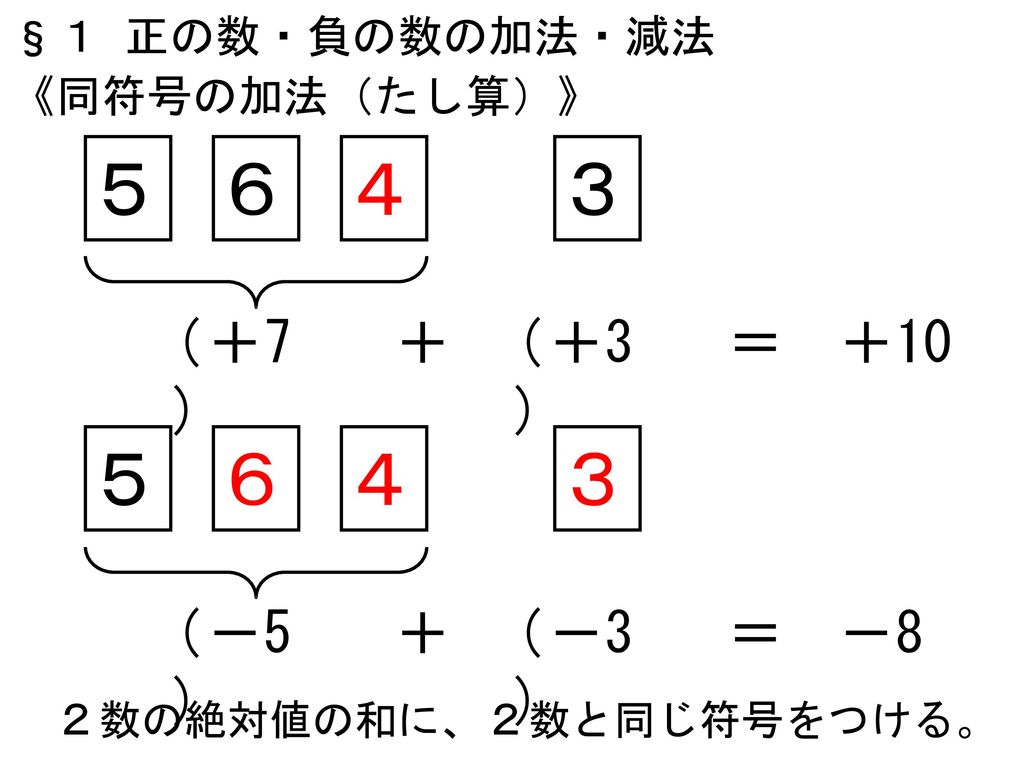



1 正の数 負の数 2章 正の数 負の数の計算 1 正の数 負の数の加法 減法 8時間 Ppt Download



2




正負の数 正負の数の減法は なぜひく数の符号を変えるのか 中学生からの勉強質問 数学 進研ゼミ中学講座
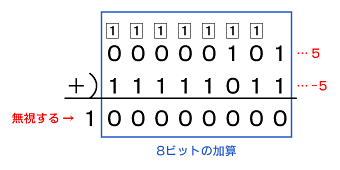



問題4 符号付き2進数と符号なし2進数 完全マスター 電子回路ドリル Ii 4 Monoist




線型代数3 置換の符号 Sgn Youtube




正負の数から乗法公式まで一気に教える




小 中必見 単元別解説 四則演算 マイナスの考え方 学習内容解説ブログ
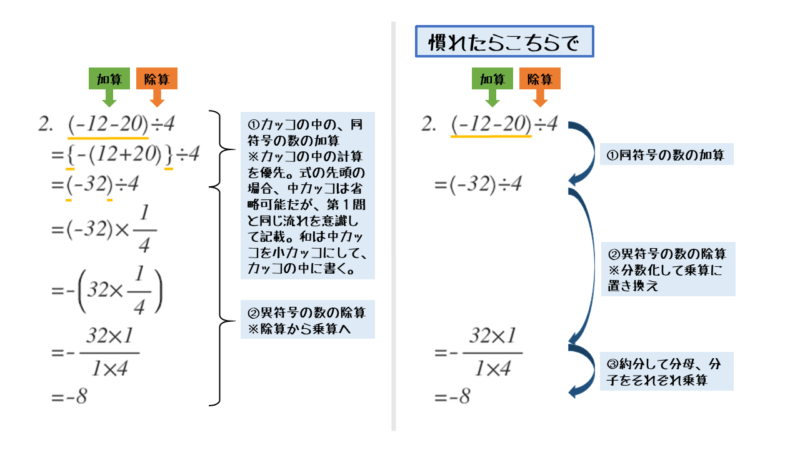



中学数学 正負の数の四則混合算を解いてみよう 日々是鍛錬 ひびこれたんれん



負の数の計算での符号ミス




中1の数学 正負の数や文字式 方程式は中学数学の基礎 家庭教師ジャニアス




分配の法則 符号ミスがなくなる決定版 中学数学の無料オンライン学習サイトchu Su




Kelas 7 Catatan Tentang 中1 四則計算 Junior Clear




中1 プラスマイナスの四則混合計算 数字は符号とセットでみる 結構よくまちがえるところ 中3でも半分くらいしか全部ちゃんとできない ここをおざなりにすると後で苦労します リアルゼミ リアルゼミ




中学数学 正負の数 でつまずく原因と解決法 加減 かっこ外し




正負の数 6 工夫して計算する 分配法則など バカでもわかる 中学数学
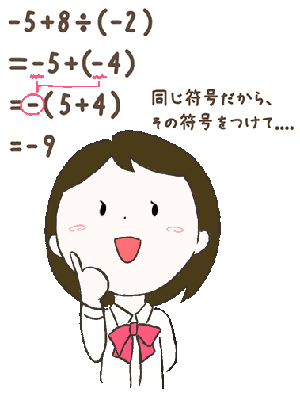



中1の数学 正負の数や文字式 方程式は中学数学の基礎 家庭教師ジャニアス




計算の符号について質問なんですが Clear



数学の質問です この文字式は何故間のマイナスもプラスにならないので Yahoo 知恵袋
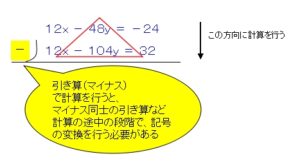



数学 連立方程式で計算ミスをしないコツ



0 件のコメント:
コメントを投稿